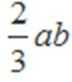理科数学德州市2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．已知集合，集合，则=（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2．若，则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

3．函数的定义域为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．已知函数，，若，则（　　）

D-1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．已知分别是定义在上的偶函数和奇函数，且，则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

10．如图所示的是函数的大致图象，则等于（　　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．已知集合，={|，，}，则集合中所有元素之和为（　）

B-2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

7．曲线在点（1，1）处切线的斜率等于（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：单选题

分值: 5分

8．若则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

9．下列四个图中，函数y=的图象可能是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．物体运动方程为，则时瞬时速度为__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

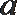
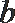
13．如图所示，已知抛物线拱形的底边弦长为，拱高为，其面积为_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

分值: 5分

14．不等式的解集为__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

15．已知为上增函数，且对任意，都有，则__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

12．已知=是奇函数，则实数的值是__________

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16．已知函数的定义域为，函数

（1）求函数的定义域；

（2）若是奇函数，且在定义域上单调递减，求不等式的解集．

正确答案

（1）由题意可知：

，

解得

∴函数的定义域为

（2）由得，

∴

又∵是奇函数，

∴

又∵在上单调递减，

∴

∴的解集为

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

18．若实数满足，则称为的不动点．已知函数，其中为常数．

（1）求函数的单调递增区间；

（2）若存在一个实数，使得既是的不动点，又是的极值点．求实数的值。

正确答案

（1）因，故．

当时，显然在上单增；

当时，由知或．

所以，当时，的单调递增区间为；

当时，的单调递增区间为，

（2）由条件知，

于是，

即，

解得

从而．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

17．已知曲线在点处的切线平行直线，且点在第三象限．

（1）求的坐标；

（2）若直线，且也过切点，求直线的方程。

正确答案

（1）由，得，

由平行直线得，解之得．

当时，：

当时，．

又∵点在第三象限，

∴切点的坐标为

（2）∵直线，的斜率为4，

∴直线的斜率为，

∵过切点，点的坐标为（－1，－4）

∴直线的方程为

即

解析

解析已在路上飞奔，马上就到！

知识点

导数的几何意义两条直线平行与倾斜角、斜率的关系两条直线垂直与倾斜角、斜率的关系直线的一般式方程

题型：简答题

分值: 12分

19．统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为：，已知甲、乙两地相距100千米

（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

正确答案

（1）当时，汽车从甲地到乙地行驶了小时，

要耗油

答当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油17．5升

（2）当速度为千米/小时时，汽车从甲地到乙地行驶了小时，设油耗为升，

依题意得（）

方法一则（）

令，解得，列表得

所以当时，有最小值．

方法二

＝11．25

当且仅当时成立，此时可解得

答：当汽车以80千米／小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11．25升．

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

21．设关于的方程有两个实根，函数．

（1）求的值；

（2）判断在区间的单调性，并加以证明；

（3）若均为正实数，证明：。

正确答案

（1）∵ 是方程的两个根，

∴ ，

∴ ，又，

∴ ，

即，同理可得

∴ ＋

（2）∵ ，

将代入整理的

又，

∴ 在区间的单调递增：

（3）∵ ，

∴

由（2）可知，

同理

由（1）可知，，，

∴

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

20．已知函数，函数

（1）当时，求函数的表达式；

（2）若，函数在上的最小值是2 ，求的值；

（3）在（2）的条件下，求直线与函数的图象所围成图形的面积．

正确答案

（1）∵ ，

∴ 当时，，

当时，，．

∴ 当时，函数．

（2）∵ 由（1）知当时，，

∴ 当时，当且仅当时取等号．

∴ 函数在上的最小值是，

∴ 依题意得∴．

（3）由解得

∴ 直线与函数的图象所围成图形的面积

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷