- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集U=R,集合M={x|x<3},N={y|y≥1},则M∩(C
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设f(x)=log


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 函数f(x)=ln(x+1)-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 若f(x)=x2 -2x-4lnx,则f′(x)>0的解集为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 函数y=3sin(

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设a,b为正实数,现有下列命题:
①若|

②若

③若a

④若|a

其中的真命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知函数y=f(x)的周期为2,当x∈[-1,1)时f(x)=x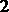
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 设向量


(Ⅰ)若


(Ⅱ)求|

正确答案
(Ⅰ)由









4sin(α+β)-8cos(α+β)=0,tan(α+β)=2.
(Ⅱ)

|





=17-30sinβcosβ=17-15sin2β,
|


所以|


解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数f(x)=


(1)求函数f(x)的解析式;
(2)解关于x的不等式;f(x)≥mx。
正确答案
(1)∵ f(x)是奇函数
∴ f(-x)=-f(x)。
即
∴ bx+c=bx-c
∴ c=0
∵ a>0,b>0
∴ f(x)=

当且仅当x=

∴ a=b
由f(1)<


∴ 2b

又 b∈N
∴ f(x)=
(2)

当m≤1时,1-m≥0,此时不等式的解集为{x|x>0}
当m>1时,
所以
综上,当m≤1时,不等式的解集为{x|x>0}
当m>1时,不等式的解集为
解析
解析已在路上飞奔,马上就到!
知识点
17. 设函数f(x)=cos(2x-

(Ⅰ)求f(x)的最大值,并写出使f(x)取最大值时x的取值集合;
(Ⅱ)已知ΔABC中,角A,B,C的对边分别为a,b,c。若f(B+C)=
正确答案
(Ⅰ)f(x)=cos(2x-



=
f(x)的最大值为2
要使f(x)取最大值,cos(2x+

故x的集合为{x|x=kπ-
(Ⅱ)由题意,f(B+C)=cos[2(B+C)+


化简得cos(2A-

∵ A∈(0,π),
∴ 2A-





在ΔABC中,由余弦定理,a




由b+c=2知bc≤(


解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,直角三角形ABC中,∠B=90°,AB=1,BC=
(Ⅰ)用θ表示线段AM的长度,并写出θ的取值范围;
(Ⅱ)求线段A′N长度的最小值。
正确答案
(Ⅰ)由对称性可知,∠NMA′=θ,则∠A′BM=π-2θ
设AM=t(0<t<1),则在直角三角形A′MB中,BM=1-t,MA′=
所以cos(π-2θ)=

(Ⅱ)在ΔAMN中,∠ANM=
当θ=

经验证,θ=
解析
解析已在路上飞奔,马上就到!
知识点
18. 定义F(x,y)=(1+x)
(Ⅰ)令函数f(x)=F(1,log





(Ⅱ)当x,y∈N
正确答案
(Ⅰ) ∵ F(x,y)=(1+x)
∴ f(x)=F(1,log2(x2-4x+9))=2
f′(x)=2x-4,过O作C
∴ 
∴ S=


(Ⅱ)证明:令h(x)=

令P(x)=
∴P′(x)=
∴ P(x)在[0,+∞)上单调递减。
∴ 当x>0时,有P(x)<P(0),∴ 当x≥1时有h′(x)<0
∴ h(x)在[1,+∞)上单调递减。
∴ 1≤x<y时,有
yln(1+x)>x ln(1+y)
∴ (1+x)
∴ 当x,y∈N
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数f(x)=
(Ⅰ)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(Ⅱ)若对
(Ⅲ)记g(x)=f(x)+x-b(b∈R),当a=1时,函数g(x)在区间[e
正确答案
(Ⅰ)直线y=x+2的斜率为1。
函数f(x)的定义域为(0,+∞),f′(x)=
所以f′(1)=
所以f(x)=
由f′(x)>0,得x>2;由f′(x)<0得0<x<2
所以f(x)的单调递增区间是(2,+∞),单调递减区间为(0,2)
(Ⅱ)f′(x)=-
∵ a>0,
由f′(x)>0得x>
所以f(x)的单调递增区间是(

当x=


∵ 对
∴ f(

∴

(Ⅲ)当a=1时,g(x)=
g′(x)=
所以g(x)的单调递增区间是(1,+∞),单调递减区间为(0,1)
x=1时g(x)取得极小值g(1)。
因为函数g(x)在区间[e

解得1<b≤
解析
解析已在路上飞奔,马上就到!
知识点
14. 设x,y为实数,若4x

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在极坐标系中,点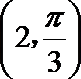
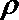
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 若直线y=2x上存在点(x,y)满足约束条件
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12. 在边长为1的正三角形ABC中,设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 如图,⊙O的弦ED,CB的延长线交于点A. 若BD⊥AE,AB=4,BC=2,AD=3,则CE=________。
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13. 若关于x的不等式4

正确答案
a≤0
解析
解析已在路上飞奔,马上就到!