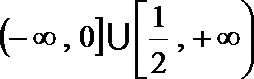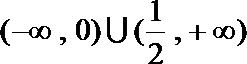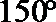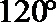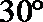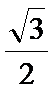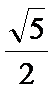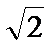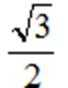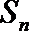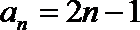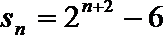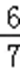- 真题试卷
- 模拟试卷
- 预测试卷
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设
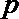


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 使函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.由直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
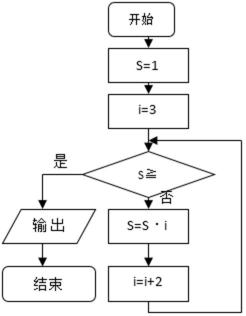
7.已知某程序框图如图所示,则输出的i的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设非零向量
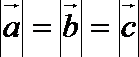

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.点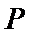
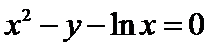
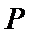
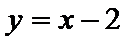
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.一个底面为正三角形且侧棱垂直于底面的三棱柱内接于半径为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.若


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.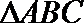
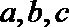
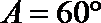
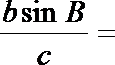
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知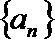
(1)求数列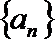
(2)若数列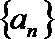
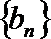

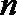

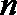
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
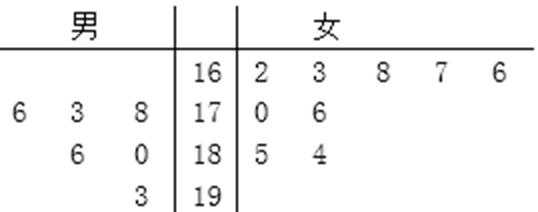
18.某航空公司进行空乘人员的招聘,记录了前来应聘的6名男生和9名女生的身高,数据用茎叶图表示如下(单位: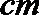
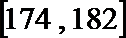
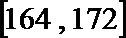
(1)求6名男生的平均身高和9名女生身高的中位数;
(2)现从能进入下一环节的应聘者中抽取2人,记X为抽取到的男生人数,求X的分布列及期望
正确答案
(1)6名男生的平均身高为
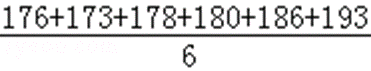
9名女生身高为162,163,166,167,168,170,176,184,185,
9名女生身高的中位数为168;
(2)男性身高在区间[174,182]的有176、178、180;
女性身高在区间[164,172]的166,167,168,170,
则X的可能取值为0,1,2,
所以
P(X=0)=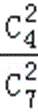
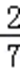
P(X=1)=
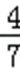
P(X=2)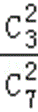
X的分布列为
期望为0×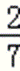
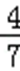
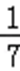
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥S-ABCD中,SD

(1)求证:平面BED
(2)求平面BED与平面SBC所成二面角(锐角)的大小
正确答案
(1)略
(2)30°
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆



(1)求椭圆C的方程
(2)求
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP、NP分别与

正确答案
(1)
(2)
(3)定值为4
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任先一题做答,如果多做,则按所做的第一题记分。
22.选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为


23.选修4-5:不等式选讲
已知函数
(1)解不等式f(x)>1
(2)求函数
24.选修4-1:几何证明选讲
如图,在



(1)求证:BE=2AD
(2)求函数AC=1,EC=2时,求AD的长
正确答案
22.
23.略
24.略
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数





(1)求
(2)设


(3)设


正确答案
(1)
(2)0<m



(3)
解析
解析已在路上飞奔,马上就到!