- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
B由题意得B=
所以A 

知识点
4.设
正确答案
解析
由题意得



所以
知识点
3.设函数

正确答案
解析
当x≤1时,21-x≤2的可变形为1-x≤1,x≥0,
∴0≤x≤1.当x>1时,1-log2x≤2的可变形为x≥
∴x≥1,
故答案为[0,+∞).故选D.
知识点
2.已知命题p: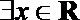
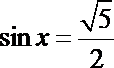
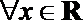
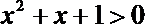
(1)命题“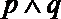
(2)命题“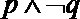
(3)命题“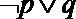
(4)命题“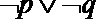
其中正确的是( )
正确答案
解析
∵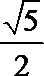
易得命题p:∃x∈R,使sin x=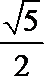
又∵x2+x+1=(x+

∴q为真命题,故非p是真命题,非q是假命题;
所以①p∧q是假命题,错;②p∧非q是假命题,正确;③非p∨q是真命题,正确;④命题“¬p∨¬q”是假命题,错;
故答案为:②③故选A.
知识点
5.若函数


正确答案
解析
∵任意给定的不等实数x1、x2,不等式(x1-x2)[f(x1)-f(x2)]<0恒成立,
∴任意实数x1、x2,满足x1<x2时有f(x1)-f(x2)>0,可得f(x)是定义在R上的减函数
∵f(x+1)是定义在R上的奇函数,
∴f(x+1)=-f(1-x)对x∈R恒成立.
令x=0,得f(1)=0
因此,不等式f(1-x)<0
即f(1-x)<f(1)
∵f(x)是定义在R上的减函数
∴1-x>1,解之得x<0,原不等式的解集为(-∞,0),故选A
知识点
7.已知函数
正确答案
解析
∵方程f(x)=ax恰有两个不同实数根,
∴y=f(x)与y=ax有2个点,
又∵a表示直线y=ax的斜率,
∴y′= 
设切点为(x0,y0),k= 
∴切线方程为y-y0=
∴y0=1,x0=e,k=

又∵直线l2与y=
∴直线l2的斜率为
∴实数a的取值范围是[

知识点
9.对于集合M、N,定义M-N={x|x∈M且x

正确答案
解析
由题可知,集合A={y|y>0},B={y|y≤2},
所以A-B={y|y>2},B-A={y|y≤0},
所以A⊕B=(-∞,0]∪ (2,+∞),故选C.
知识点
6.在ΔABC中,角A,B,C所对应的边分别为a,b,c,则“a≤b”是“sinA≤sinB”的( )
正确答案
解析
由正弦定理得
若“a≤b”则“sin A≤sin B”,即充分性成立,
若“sin A≤sin B”则“a≤b”成立,即必要性成立,
故“a≤b”是“sin A≤sin B”的充要条件,故选C
知识点
8.已知函数


正确答案
解析
因为x>-1, 
所以x+1>0,
所以由均值不等式得y
当且仅当x+1=

所以x+1=3,x=2时等号成立,
所以a=2,

知识点
10. 已知方程
正确答案
解析
∵方程
∴方程
∴函数y=|sinx|和函数y=kx在(0,+∞)上有两个交点,作出两个函数的图象,
函数y=|sinx|和函数y=kx在(0,π)上有一个交点A(a,sina),
在(π,2π)上有一个切点B(b,sinb)时满足题意,a,b是方程的根.
当x∈(π,2π)时,f(x)=|sinx|=-sinx,f′(x)=-cosx,
∴在B处的切线为y-sinb=f′(b)(x-b),将x=0,y=0代入方程,得sinb=-bcosb,
∴


∴
知识点
11.若(a+1)

正确答案
(

解析
∵


∴a+1>3-2a>0,解得


知识点
14.已知f(x)定义在(0,+∞)的可导函数,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 非空集合G关于运算⊕满足:(1)对任意




现给出下列集合和运算:
①G={非负整数},⊕为整数的加法。
②G={偶数},⊕为整数的乘法。
③G={平面向量},⊕为平面向量的加法。
④G={二次三项式},⊕为多项式的加法。
⑤G={虚数},⊕为复数的乘法。
其中G关于运算⊕为“融洽集”的是__________。
正确答案
①③
解析
①G={非负整数},⊕为整数的加法,满足任意a,b∈G,都有a⊕b∈G,且令e=0,有a⊕0=0⊕a=a,∴①符合要求;
②G={偶数},⊕为整数的乘法,若存在a⊕e=a×e=a,则e=1,矛盾,∴②不符合要求;
③G={平面向量},⊕为平面向量的加法,两个向量相加结果仍为向量;取e=
④G={二次三项式},⊕为多项式的加法,两个二次三项式相加得到的可能不是二次三项式,∴④不符合要求;
⑤G={虚数},⊕为复数的乘法,两个虚数相乘得到的可能是实数,∴⑤不符合要求,这样G关于运算⊕为“融洽集”的有①③.故答案为:①③.
知识点
13.设函数f(x)= 
正确答案
4
解析
由已知定义域为{x|x∈R且x≠±1}
原函数可化为
设f(x)=


结合定义域可知该函数为奇函数,设f(x)的最大值为t,结合图象可知其最小值为-t,
所以对原函数而言M=2+t,m=2-t,所以M+m=4.故答案为:4
知识点
12. 设f(x)=lg,则
正确答案
(-4,-1)
解析
由题意得f(x)的定义域为(2,+ 


所以



所以

知识点
16.集合



正确答案
因为A=[1,8],又A⊆B,
所以lnx-ax+2>0,在x∈[1,8]上恒成立,
即
令g(x)=

所以g(x)min=g(8)= 

解析
解析已在路上飞奔,马上就到!
知识点
18.函数f (x) 对一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f (1)=0
(Ⅰ)求f (0)的值;
(Ⅱ)求函数f(x)的表达式;
(Ⅲ)对于任意的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求函数的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值


(3)若过点M(2,



正确答案
(1)f(x)=
(2)f'(x)=3ax2+2bx﹣3.
根据题意,得
即
所以f(x)= 
当

当

因为f(-1)=2,f(1)=-2,所以当

对于区间


所以c
(3)因为点M(2,m)(m≠2)不在曲线y=f(x)上,
所以可设切点为(x0,y0).则y0=x03﹣3x0.
因为f'(x0)=3x02﹣3,所以切线的斜率为3x02﹣3.则3x02﹣3=
即2x03﹣6x02+6+m=0.
因为过点M(2,m)(m≠2)可作曲线y=f(x)的三条切线,
所以方程2x03﹣6x02+6+m=0有三个不同的实数解.
所以函数g(x)=2x3﹣6x2+6+m有三个不同的零点.
则

当


当


有方程与函数的关系要满足题意必须满足
解得-6<m<2
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=xlnx,g(x)=x-1(e≈2.71828)
(Ⅰ)求函数h(x)=f(x)-g(x)的极小值;
(Ⅱ)已知
正确答案
(Ⅰ)解:由题意得h(x)=f(x)-g(x)=xlnx-x+1,则h′(x)=lnx,
令h′(x)>0,得x>1,令h′(x)<0,得0<x<1,
∴h(x)的增区间为(1,+∞),减区间为(0,1).
∴函数h(x)=f(x)-g(x)的极小值为h(1)=0.
(Ⅱ)证明:∵f(b)=f(a),又
∴blnb=a-1>0,则lnb>0,得b>1.
同理由f(c)=g(b),得clnc=b-1>0,则c>1.
∵a-b=g(a)-g(b)=f(b)-g(b)=h(b),
又b>1由(Ⅰ)知a-b=h(b)>h(1=0,
同理,b-c=h(c)>0,则有1<c<b<a<2,
设h(x)=

令ω(x)=x-1-lnx,1<x<2,
则ω′(x)=
h(x)在(1,2)上单调增加,∴h(x)<h(2)=ln4,∴4<e
∴h(x)<ln4<



同理






c-1>







解析
解析已在路上飞奔,马上就到!
知识点
17.设

(1)若

(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数f(x)=ax+xlnx的图象在点x=e(e为自然对数的底数)处的切线的斜率为3
(1)求实数a的值;
(2)若f(x)≤kx2对任意x>0成立,求实数k的取值范围;
(3)当n>m>1(m,n∈N*)时,证明:
正确答案
(1)因为f(x)=ax+xlnx,所以f'(x)=a+lnx+1.
因为函数f(x)=ax+xlnx的图象在点x=e处的切线斜率为3,
所以f'(e)=3,即a+lne+1=3.所以a=1.
(2)由(1)知:


则

则




∴


∴

(3)构造函数
h(x)=xlnx-x+1,o<x<1,则
所以h(x)>h(1)=0 所以
又n>m>1,所以0< 

即




即



即
即

解析
解析已在路上飞奔,马上就到!













































