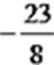- 真题试卷
- 模拟试卷
- 预测试卷
4.已知函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,棋盘式街道中,某人从A地出发到达B地.若限制行进的方向只能向右或向上,那么不经过E地的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 程序框图如图:如果上述程序运行的结果S=1320,那么判断框中应填入( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在正三棱柱ABC—A1B1C1中,若AB=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.对于集合M、N,定义:





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知



正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
12.双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.一个口装中有编号为1、2、3、4、5的五个大小形状完全一样的小球,现从袋中同时摸出



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设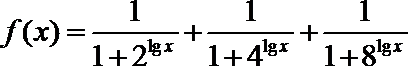
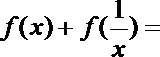
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
14.已知某个几何体的三视图如图所示,根据图中标出的尺寸,则这个几何体的体积是( ).
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
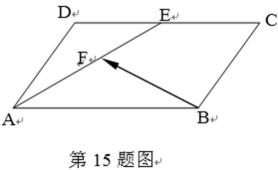
15. 在平行四边形ABCD中,AB=3,AD=2,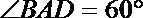
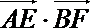
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.正三棱锥


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数

(1)若

(2)在△ABC中,若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知等比数列









(1)求数列

(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,四棱锥P-ABCD中,PA⊥底面ABCD,





(1)求证:BC⊥平面PAC;
(2)求异面直线AC与PD所成的角的余弦值
(3)试确定点M的位置,使直线MA与平面PCD所成角

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知中心在原点,焦点在



(1)求椭圆方程;
(2)设不过原点O的直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)如果

(2)如果



(i)求证:
(ii)求证:
正确答案
解析
解析已在路上飞奔,马上就到!