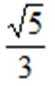- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合M={x|x2﹣1≤0},N={x|
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设x>0,y>0,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若A为不等式组


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下列命题中:
①“x>|y|”是“x2>y2”的充要条件;
②若“∃x∈R,x2+2ax+1<0”,则实数a的取值范围是(-∞,-1)∪(1,+∞);
③已知平面α,β,γ,直线m,l,若α⊥γ,γ∩α=m,γ∩β=l,l⊥m,则l⊥α;
④函数f(x)=(



其中正确的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某教师一天上3个班级的课,每班开1节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5节和第6节不算连上),那么这位教师一天的课表的所有排法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个实数根,则t的取值范围为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.从1,2,3,4,5中任取2个不同的数,事件A=“取到的2个数之和为偶数”,事件B=“取到的2个数均为偶数”,则P(B|A)等于
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
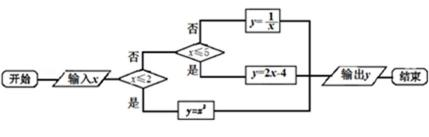
12.如图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
14.已知在平面直角坐标系中,A(-2,0),B(1,3),O为原点,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设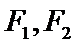
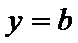
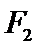
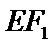
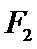

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.
(Ⅰ)求这4位乘客中至少有一名乘客在第2层下电梯的概率;
(Ⅱ) 用

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.等差数列







(1)求通项公式

(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)当

(2)已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆




(Ⅰ)求椭圆
(Ⅱ)过原点的直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 设函数

(1)讨论
(2)若








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 如图,已知菱形







(Ⅰ)若点



(Ⅱ)求二面角
(Ⅲ)设点



正确答案
解析
解析已在路上飞奔,马上就到!