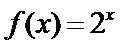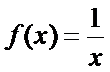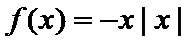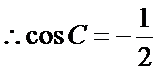- 真题试卷
- 模拟试卷
- 预测试卷
1. 复数

正确答案
解析
复数

考查方向
解题思路
1.先利用复数的运算法则化简复数;2.根据复数的虚部的概念即可得到答案。
易错点
1:不理解虚部是什么误选A; 2复数运算出错。
知识点
4.设双曲线

正确答案
解析
双曲线a=2,b=1,c=





考查方向
解题思路
1.根据双曲线方程求出双曲线的基本量a,b,c;2.利用双曲线的定义得到
易错点
1。
知识点
5. 下列有关命题说法正确的是 ( )
正确答案
解析
对于A选项,








考查方向
解题思路
逐个选项判断正误即可。
易错点
1.不明白充分必要条件误选B;2.对于D选项中的对数函数的增减性弄错导致出错。
知识点
7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,
这6名学生要排成一排合影,则同校学生排在一起的概率是 ( )
正确答案
解析
由已知把第一个及第二个学校的学生看做整体得同校学生排在一起共


考查方向
解题思路
1.先求出把第一个及第二个学校的学生看做整体得同校学生排在一起共

易错点
不会相邻问题如何处理;
知识点
9.若某几何体的三视

正确答案
解析
该几何体是三棱柱



考查方向
解题思路
1.先根据三视图还原成原来的几何体为三棱柱


易错点
1.不会根据三视图还原原来的几何体形状;2.不知道如何求不规则的几何体的体积导致割补出错。
知识点
2. 下列函数在其定义域上既是奇函数又是减函数的是 ( )
正确答案
解析
A中
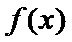

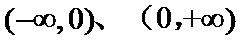
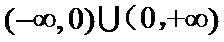

考查方向
解题思路
1.先根据奇偶性判断排除A,B;
易错点
误认为C中反比例函数在定义域上单调递减而选择C。
知识点
3. 已知


正确答案
解析




所以

考查方向
解题思路
1.先根据题中条件求出角
易错点
1.利用诱导公式在化简时出错;2.对于特殊角的三角函数值记忆出错。
知识点
6. 将函数



正确答案
解析










考查方向
解题思路
1.先根据函数图像的平移得到函数
易错点
1. 误将函数

到
知识点
8.执行如图8的程序框图,若输出


正确答案
解析
第1次运算:









考查方向
解题思路
根据给出的程序框图循环执行,后发现
易错点
1.无法确定程序结束的条件导致出错;2.不将程序运行完成就退出程序导致出错。
知识点
10.若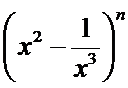
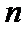
正确答案
解析
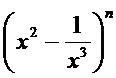
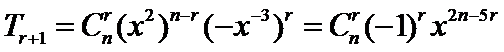
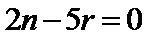
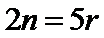
考查方向
解题思路
1.先写出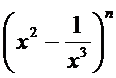
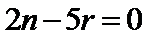
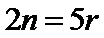
易错点
1.展开式中的通项公式易丢掉-1导致出错;
2.对于通项公式的化简即指数幂的运算出错,不知道题中存在常数项是什么意思。
知识点
11.
正确答案
解析

又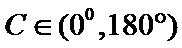
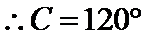
考查方向
解题思路
1。先根据题中给出的向量的数量积求出
2.利用已知三角函数值求出角C的大小。
易错点
1.对于向量的知识掌握不好,以为向量和数量一样出错;
2.对于特殊角的三角函数值记忆出错。
知识点
12. 形如





正确答案
解析
令






所以 


所以 


在同一坐标系内的图象如图所示,图像交点个数为4 ,选C
考查方向
解题思路
1.先根据

2.根据“囧函数”的概念求出
3.在同一个坐标系下做出

易错点
1.不理解题中给出的“囧函数”的概念;
2.不会处理复合函数函数
知识点
13.一个长方体高为5,底面长方形对角线长为12,则它外接球的表面积为
正确答案
解析
如图,长方体
它外接球直径2R=
外接球的表面积为
考查方向
解题思路
1.先根据长方体的知识求出外接球的半径;
2.根据球的体积公式求出球的表面积。
易错点
1.不知道长方体的外接球的半径如何求;
2.可能误将求表面积求成体积出错。
知识点
14.如图,探照灯反射镜的纵截面是抛物线的一部分,光源在抛物线的焦点F处,灯口直径AB为



正确答案


解析
.建立如图平面直角坐标系,设抛物线方程为
则点A(40,30)在抛物线上, 

考查方向
解题思路
1.建立平面直角坐标系设出抛物线的方程;
2.根据题意点A(40,30)在抛物线上求出p;
易错点
不会将题中给出的应用问题建立坐标系求解;
知识点
15.已知点


正确答案
解析


与点M(-1,0)的距离的平方,由图知:
M到直线

由于

考查方向
解题思路
1.先根据题中给出的约束条件画出可行域;2. 

易错点
1.在画可行域的时候画错;
2.不会转化题中的目标函数
知识点
16.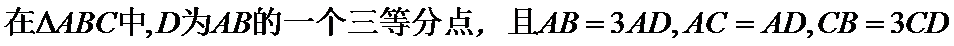
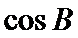
正确答案
解析
令AC=AD=1,CD=x > 0 , 则 AB=3 , BC= 3x ,
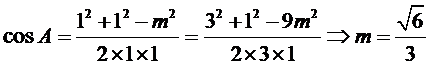
考查方向
解题思路
1.先设出题中需要的线段的长度;
2.根据余弦定理求出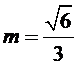
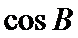
易错点
1.不会设出长度解决问题;
2.不会利用角A的余弦构造方程解方程。
知识点
如图,












21.求证:
22.求平面

正确答案
(1)略;
解析
解:

而




考查方向
解题思路
先证明
易错点
找不到
正确答案
(2)
解析
设




易知








同理
二面角









考查方向
解题思路
先证明


易错点
找不到二面角的平面角无法做出答案。
已知椭圆



23.求椭圆C的方程;
24.设不过原点O的直线
PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围。
正确答案
(1)
解析
:(1) 由直线



由

又

椭圆C的方程为
考查方向
解题思路
问先根据


易错点
不会转化

正确答案
(2)(0,1)
解析
:
(2)由题意可知,直线
y=kx+m(m≠0),P(x1,y1),Q(x2,y2),
由消去y得(1+4k2)x2+8kmx+4(m2-1)=0,
则Δ=64k2m2-16(1+4k2)(m2-1)=16(4k2-m2+1)>0,
且x1+x2=,x1x2=.
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以·==k2,
即+m2=0, 又m≠0,所以k2=,即k=±.
由Δ>0,及直线OP,OQ的斜率存在,得0<m2<2且m2≠1.
S△OPQ=|x1-x2||m|= 
所以S△OPQ的取值范围为(0,1).
考查方向
解题思路
设出直线


易错点
不会转化OP,PQ,OQ的斜率依次成等比数列导致问题找不到突破口。
已知


17.求数列
18.求数列


正确答案
(1)
解析
(1) 设



由


考查方向
解题思路
利用等差数列的性质求出数列
易错点
利用等差数列的性质求通项公式和等比数列的性质混淆;
正确答案
解析
(2)
由
得
① -②得

又
当


考查方向
解题思路
根据公式构造等式求出
易错点
先构造等式做差后求出
我国新发布的《环境空气质量标准》指出:空气质量指数在




量指数频率分布直方图,如图.
19.求
20. 如果空气质量指数不超过



正确答案
(1)
解析
(1)由题意,得
解得
50个样本中空气质量指数的平均值为
可估计2015年这一年度空气质量指数的平均值约为24.6
考查方向
解题思路
根据频率分布直方图求出a的值,然后根据平均数的求法求出2015年这一年度空气质量指数的平均值约为24.6;
易错点
不会根据频率分布直方图估计平均数;
正确答案
(2)


解析
(2)利用样本估计总体,该年度空气质量指数在





考查方向
解题思路
根据题意判断出
易错点
看不出二项分布导致运算很麻烦。
已知定义在R上的偶函数


25.当

26.求最大的整数



正确答案
(1)
解析
(1):当


记过原点与

则切线L斜率为
又切线过(0,0),所以



∴当



考查方向
解题思路
先设切点后利用导数的几何意义求出切点坐标后即得切线方程;
易错点
没有给出切点导致无法入手;
正确答案
(2)4
解析
(2)因为任意

当


当


∴ 

又整数


得:

∴ 

令

当


当


又


由此可见,方程


且当






下面证明:

①当




②当

令




∴

综上所述,

考查方向
解题思路
先探求出m的值后证明。
易错点
对于题中给的信息无法处理导致没有思路。
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,
直线
27. 求证:

28.求圆
正确答案
(1)略;
解析
(I)如图22-1,由切割线定理得







考查方向
解题思路
先根据切割线定理求出

易错点
不会根据切割线定理求解;
正确答案
(2)4
解析
(2):如图22-2连结



设













考查方向
解题思路
先证明
易错点
不会做辅助线导致无法求出正确答案。