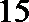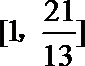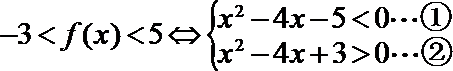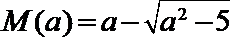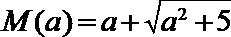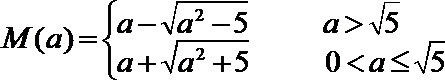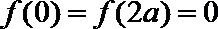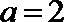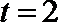- 真题试卷
- 模拟试卷
- 预测试卷
6.设等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图的程序框图运行后输出的结果是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11 .已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若函数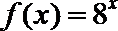
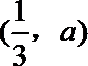
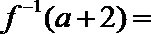
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知复数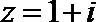
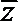
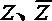
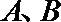

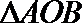
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
5.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若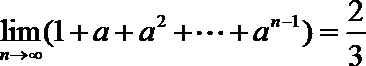
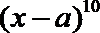
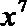
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10 . 一个盒子装有六张卡片,上面分别写着如下六个函数:






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数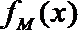
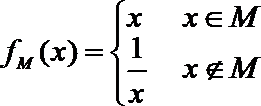
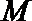
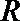
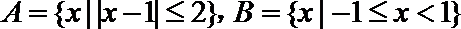
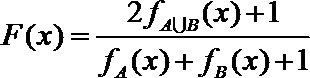
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图所示,四棱锥





① 若



② 若

③ 若


④若



其中正确的命题是 ( )
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
2.线性方程组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若实数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设





(1)若

(2)若



正确答案
设





(1)若

(2)若



证明:(证法一)(1)∵


由正弦定理可知,


∴

(证法二)∵


由正弦定理可知,
∵


(2)由题意可知,

由余弦定理可知,


∴
解析
解析已在路上飞奔,马上就到!
知识点
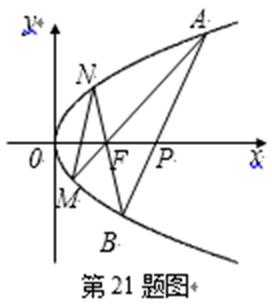
21.如图,已知抛物线






(1)证明
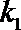


(2)记直线
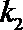

正确答案
证明:(1)依题意,设直线

将其代入

整理得 
从而
于是
∴

又
(2)证明:设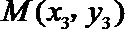
则 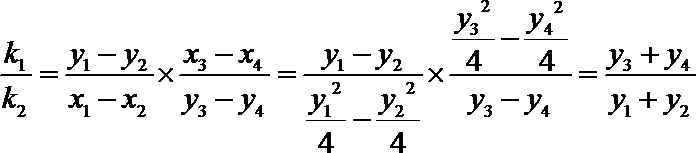
设直线

将其代入

整理得
∴
同理可得 
故
由(1)知,
∴
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数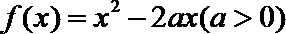
(1)当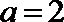
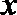
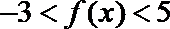
(2)对于给定的正数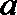



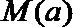
(3)函数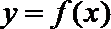
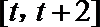

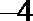
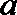
正确答案
(1)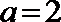
由①得,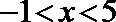
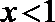
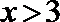
∴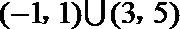
(2)∵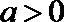
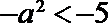
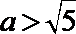
当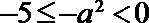
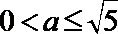
∴
(3)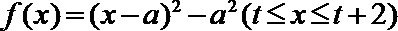
①若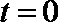
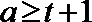
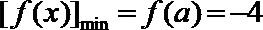
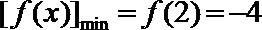
当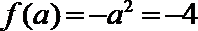
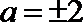
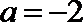
当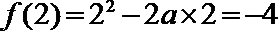
②若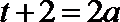
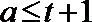
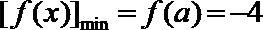
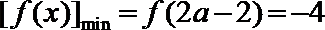
当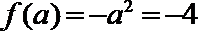
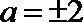
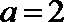
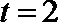
若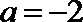
当
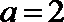
综上所述,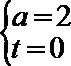
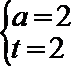
解析
解析已在路上飞奔,马上就到!
知识点
23.一青蛙从点





(1)若点





(2)若点




(3)若点




正确答案
(1)设
所以

(2) 依题意,
随着

(方法二)∴



又
∴
于是,当
当
∴
解析
解析已在路上飞奔,马上就到!
知识点
20.空气污染指数(API)是一种用于反映和评价空气质量的数量,我国计入空气污染指数的项目暂定为:总悬浮颗粒物(











(1)若某地区的





(2)已知某地的首要污染物为












正确答案
(1)设





根据上表,对于

∴
其API分指数为
同理

由此可见,空气污染指数API为
(2)依题意,
解得

∴限排后



解析
解析已在路上飞奔,马上就到!