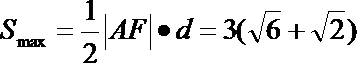- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.给定两个命题




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.为了得到函数y=sin 3x+cos 3x的图像,可以将函数y=cos 3x的图像( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.一个几何体的三视图如图所示(单位:m),则该几何体的体积为_____________m3
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知圆C的圆心C在抛物线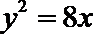
(1)求圆C的方程;
(2)设圆C与抛物线的准线的公共点为A,M是圆C上一动点,求三角形ΔMAF的面积的最大值。
正确答案
(1)解法一:设圆的方程为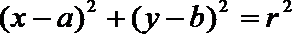
由题意可得: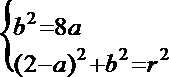
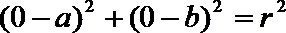
解得: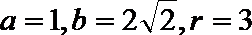
所以圆的方程是: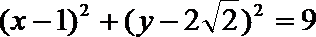
解法二:由题知,圆心在线段OF的中垂线x=1上;
由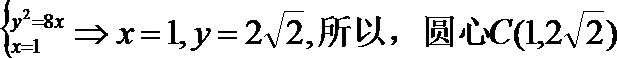
半径r=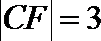
所以圆的方程是: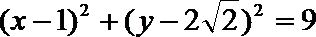
(2)由题知:当点M在AF的中垂线与圆的上交点处时,ΔMAF的面积最大。
由抛物线定义知:圆C与抛物线的准线x=-2相切,切点A(-2,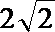
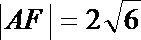

直线AF的方程是: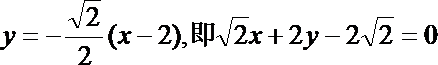
圆心C到直线AF的距离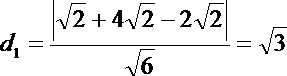
点M到直线AF的最大距离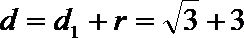
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在长方体

(1)求证:D1E⊥A1D;
(2)求AB的长度;
(3)在线段AB上是否存在点E,使得二面角
正确答案
(1)证明:连结AD1,由长方体的性质可知:AE⊥平面AD1,又∵AD=AA1=1, ∴AD1⊥A1D 所以,A1D⊥平面AD1E ∴D1E⊥A1D1;
(2)
设AB=x,
∵四边形ADD1A是正方形,
∴小蚂蚁从点A沿长方体的表面爬到点C1可能有两种途径,
如图甲的最短路程为
如图乙的最短路程为

(3)假设存在连结DE,设EB=y,
过点D在平面ABCD内作DH⊥EC,连结D1H,
则∠D1HD为二面角

即
解法二: (1)如图建立空间坐标系设AE=a
则E(1,a,0), D1(0,0,1)],A1(1,0,1)

(2)同解法一
(3)假设存在, 平面DEC的法向量
设平面D1EC的法向量


由题意得:
解得:
解析
解析已在路上飞奔,马上就到!
知识点
20.函数
(I)若函数


(II)若函数


(III)求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设椭圆C1:

(1)求椭圆C1的方程;
(2)设M(0,

正确答案
(1)解:由题意可知B(0,-1),则A(0,-2),故b=2.
令y=0得

所以

(2)设N(



代入椭圆方程整理得:




故

设点M到直线PQ的距离为d,则
所以,


当

综上可知,

解析
解析已在路上飞奔,马上就到!
知识点
19.观察下列三角形数表,假设第

(1)依次写出第六行的所有
(2)归纳出

(3)设

正确答案
(1)第六行的所有6个数字分别是6,16,25,25,16,6;
(2)依题意



所以
(3)因为
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


(1)求函数
(2)在△






正确答案
(1)
由

∴
(2)由



∴



再由余弦定理得,
解析
解析已在路上飞奔,马上就到!