理科数学广州市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2.已知函数①y=sinx+cosx，②y=sinxcosx，则下列结论正确的是（）

A两个函数的图象均关于点(-，0)成中心对称

B两个函数的图象均关于直线x=-成轴对称

C两个函数在区间(-)上都是单调递增函数

D两个函数的最小正周期相同

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：单选题

分值: 5分

3.设f(x)=,则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

5.下列四个命题中，正确的是（）

A已知服从正态分布N(0，2)，且P(-2≤≤0)=0.4，则P（>2）=0.2

B设回归直线方程为y=2-2.5x，当变量x增加一个单位时，y平均增加2个单位

C已知命题p：x∈R，tanx=1；命题q：x∈R，x2-x+1>0．则命题“p﹁q”是假命题

D已知直线l1：ax+3y-1=0,l2：x+by+1=0，则l1l2的充要条件是 =-3

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

8.设函数f(x)的定义域为R，若存在常数M>0使对一切实数x均成立，则称函数f(x)为F函数．现给出下列函数：

①f(x）=x2

②f(x)=

③f(x)=x(1-2x)

④f(x)是定义在实数集R上的奇函数，且对一切x1x2均有．

其中是F函数的序号为（）

A① ② ③

B② ④

C② ③

D③ ④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

1.已知集合A={x∈R|x<5-}，B={1，2，3，4)，则(CRA)B=（）

A{1，2，3，4}

B{2，3，4}

C{3，4}

D{4}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

4.一个三棱柱的底面是正三角形，侧棱垂直于底面，它的三视图及其尺寸如下(单位cm)，则该三棱柱的表面积为（）

A(24+8)cm2

B24cm2

Ccm2

Dcm2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

7.已知k∈=(k,1),=(2,4)，若≤,则△ABC是直角三角形的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像与性质

题型：单选题

分值: 5分

6.给出30个数：1，2，4，7，11，……其规律是

第一个数是1，

第二个数比第一个数大1，

第三个数比第二个数大2，

第四个数比第三个数大3，……

以此类推，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框①处和执行框②处应分别填入（）

Ai≤30?；p=p+i-1

Bi≤29?；p=p+i+1

Ci≤31?：p=p+i

Di≤30?；p=p+i

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

10.若实数x，y满足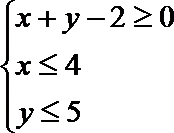，则s=y-x的最小值为________

正确答案

-6

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：填空题

分值: 5分

9.i是虚数单位，的共轭复数的数是________.

正确答案

-1-i

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算

题型：填空题

分值: 5分

12.已知数列{an}的前n项和Sn=n2-7n，且满足16<ak+ak+1<22，则正整数k=_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

13.已知函数f(x)=-alnx(a∈R)，若函数f(x)在[1,2]为增函数，且f/(x)在[1，2]上存在零点(f/(x)为f(x)的导函数)，则a的值为___________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 5分

11.已知()n展开式的第4项为常数项，则展开式中各项系数的和为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：填空题

分值: 5分

选做题（14、15题，考生只能从中选做一题）

14.（极坐标与参数方程选做题）

已知曲线C的极坐标方程是，直线l的参数方程是(t为参数).设直线l与x轴的交点是M，N是曲线C上一动点，则MN的最大值为____________

15.（几何证明选讲选做题）

如图，⊙O中，直径AB和弦DE互相垂直，C是DE延长线上一点，连结BC与圆0交于F，若∠CFE=()，则∠DEB___________

正确答案

14.

15. a

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直与倾斜角、斜率的关系

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16.已知函数f(x)=2sin(>0,0<)的最小正周期为，且f.

（1）求的值；

（2）若f

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：简答题

分值: 12分

17.如图，P-AD-C是直二面角，四边形ABCD是∠BAD=1200的菱形，AB=2，PA ⊥ AD，E是CD的中点，设PC与平面ABCD所成的角为450．

（1）求证：平面PAE⊥平面PCD；

（2）试问在线段AB(不包括端点)上是否存在一点F，使得二面角A-PE-D的大小为450?若存在，请求出AF的长，若不存在，请说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：简答题

分值: 14分

21.已知a为实数，数列满足a1 =a,当n≥2时，an =

（1）当a=100时，求数列{an}的前100项的和S100；

（2）证明：对于数列{an}，一定存在k∈N*，使0<ak≤3；

（3）令bn=,当2＜a＜3时，求证：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：简答题

分值: 14分

18.某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动)．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

（1）求合唱团学生参加活动的人均次数；

（2）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率；

（3）从合唱团中任选两名学生，用ξ 表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ ．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的作用

题型：简答题

分值: 14分

20.已知函数f(x)=(x∈R，a，b为实数)有极值，且在x=1处的切线与直线x-y+1=0平行．

（1）求实数a的取值范围；

（2）是否存在实数a，使得函数(x)的极小值为1，若存在，求出实数a的值；若不存在，请说明理由；

（3）设a=,f(x)的导数为f/(x),令g(x)=求证：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

n次独立重复试验中恰好发生k次的概率

题型：简答题

分值: 14分

19.已知过点A(0，4)的直线l与以F为焦点的抛物线C：x2=py相切于点T(-4，yo)；中心在坐标原点，一个焦点为F的椭圆与直线l有公共点．

（1）求直线l的方程和焦点F的坐标；

（2）求当椭圆的离心率最大时椭圆的方程；

（3）设点M(x1，yl)是抛物线C上任意一点，D(0,-2)为定点，是否存在垂直于y轴的直线l/被以MD为直径的圆截得的弦长为定值?请说明理由．

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷