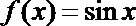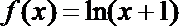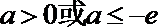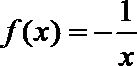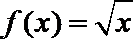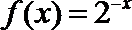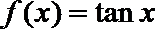- 真题试卷
- 模拟试卷
- 预测试卷
11.已知函数



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
12.若函数



正确答案
1;
解析
解析已在路上飞奔,马上就到!
知识点
9.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,线段








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对于函数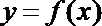
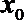
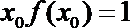
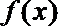
(1)下列函数中具有性质P的有___________.
①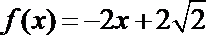
②
③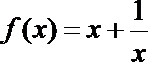
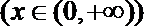
④
(2)若函数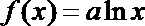
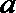
正确答案
(1) ①②④,(2)
解析
解析已在路上飞奔,马上就到!
知识点
2.下列函数中,在定义域内是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知集合




①

②

③

④

其中,正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知点P是函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设






正确答案
P真:

解析
解析已在路上飞奔,马上就到!
知识点
16.如图,已知点







(I)求函数
(II)求函数
正确答案
(I)由已知
所以

(II)解:
由

函数

所以当


解析
解析已在路上飞奔,马上就到!
知识点
17.在△


(Ⅰ)求
(Ⅱ)若

正确答案
(Ⅰ)解:由

所以 
即 
因为 

所以 
(Ⅱ)解:由



所以 
由正弦定理得 

所以 △

解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(Ⅰ)若


(Ⅱ)求函数
(Ⅲ)求证:
正确答案
(Ⅰ)易证
(Ⅱ)当


当



(Ⅲ)要证

由(Ⅰ)可知,

得到
将上述

从而结论成立.
解析
解析已在路上飞奔,马上就到!
知识点
19.已知抛物线




(Ⅰ)求抛物线
(Ⅱ)设点








(Ⅲ)过(Ⅱ)中的点








正确答案
(Ⅰ)
(Ⅱ)直线

(Ⅲ)点
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列




(Ⅰ)若

(Ⅱ)求证:
(Ⅲ)当


正确答案
解:(I)27,9,3;8,9,3;6,2,3.
(II)若


若



若


所以
所以
所以,对于数列



因为

所以数列

若





由递推关系易得
(III)集合

由已知递推关系可推得数列
当


下面考虑当

按逆序排列各项,构成的数列记为

由(II)的证明过程可知数列




所以,满足



所以



所以



因为


所以


解析
解析已在路上飞奔,马上就到!