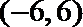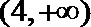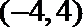- 真题试卷
- 模拟试卷
- 预测试卷
4. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一次实验:向下图所示的正方形中随机撒一大把豆子,经查数,落在正方形中的豆子的总数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 在复平面内与复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设等比数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知命题







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 执行如图所示的程序框图,则输出结果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知实数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.四面体






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数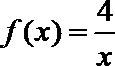
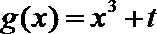
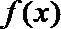
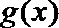
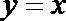
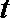
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,某几何体的主视图和俯视图都是矩形,左视图是等腰直角三角形,则该几何体的体积为__________.
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知抛物线




正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
17. 设数列







(1)求数列

(2)设



正确答案
(1)由已知条件得
当

①-②得:
即
∵数列


又


∴

(2)∵
∴

两式相减得
∴
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知向量



(1)求函数

( 2)将函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁. 私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力. 为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
Ⅰ.完成被调查人员的频率分布直方图;
Ⅱ.若从年龄在[15,25. ,[25,35. 的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为

正确答案

所以
所以

解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在四棱锥







( 1)求证:平面

(2)设




正确答案
(1)










(2) 

又


建系







平面




解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆



( 1)求椭圆
(2)设点









正确答案
(1)依题意,设椭圆C的方程为=1(a>b>0),焦距为2c,
由题设条件知,a2=8,b=c, 所以b2=
故椭圆C的方程为
(2)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
显然直线l的斜率k存在,所以直线的方程为y=k(x+4)。
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的
中点为G(x0,y0),
由
得(1+2k2)x2+16k2x+32k2-8=0 ①
由=(16k2)2-4(1+2k2)(32k2-8)>0
解得

因为x1,x2是方程①的两根,所以x1+x2=-
于是x0=

∵x0=
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为

解得

故直线l斜率的取值范围是[

解析
解析已在路上飞奔,马上就到!
知识点
22. 设

(Ⅰ)求




(Ⅱ)设



正确答案
(Ⅰ)∵
∴
由题意得:

∴
令

∵

∴
故

(1)当



由


(2)当



由


(Ⅱ)由(Ⅰ)知:当







解析
解析已在路上飞奔,马上就到!