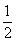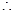- 真题试卷
- 模拟试卷
- 预测试卷
3. 
正确答案
解析
知识点
4.图中,



正确答案
解析
根据提供的该算法的程序框图,该题的最后得分是三个分数中差距小的两个分数的平均分.根据







知识点
9.下列命题中正确的有( )
①设有一个回归方程
②命题P:“


③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-1<X<0)=
④在一个2×2列联表中,由计算得k2=6.679,则有99%的把握确认这两个变量间有关系.
本题可以参考独立性检验临界值表
正确答案
解析
①变量x增加一个单位时,y平均减少3个单位,所以错误。②正确。③
知识点
2.函数
正确答案
解析
∵余弦函数
∴函数
知识点
5.长方体一个顶点上的三条棱长分别为3、4、5,若它的八个顶点都在同一个球面上,则这个球的表面积是( )
正确答案
解析
易知长方体外接球的半径为

知识点
7.对于函数




正确答案
解析
对于函数




选项B、C、D函数没有对称轴;函数f(x)=cos(x+1),有对称轴,且x=0不是对称轴,选项A正确.
知识点
1.若全集U=R,集合A={x|x2+x﹣2≤0},B={y|y=log2(x+3),x∈A},则集合A∩(∁UB)=( )
正确答案
解析
A={x|x2+x﹣2≤0}={x|﹣2≤x≤1},
∵B={y|y=log2(x+3),x∈A},由于函数y=log2(x+3)为增函数,
∴B={y|0≤y≤2},
∵全集U=R
∴∁UB={y|y<0或y≥2},
∴A∩∁UB={x|﹣2≤x<0}.
故选:A.
知识点
8.下面命题中假命题是( )
正确答案
解析
A根据指数函数的性质可知,∀x∈R,3x>0,∴A正确.
B当α=β=0时,满足sin(α+β)=sinα+sinβ=0,∴B正确.
C当m=1时,幂函数为f(x)=x3,且在(0,+∞)上单调递增,∴C正确.
D命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”,∴D错误.
故选:D.
知识点
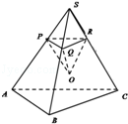
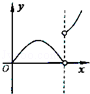
10.如图,在棱长为1正四面体S﹣ABC,O是四面体的中心,平面PQR∥平面ABC,设SP=x(0≤x≤1),三棱锥O﹣PQR的体积为V=f(x),其导函数y=f(x)的图象大致为( )
正确答案
解析
设O点到底面PQR距点0的高为h,底面PQR的面积为s,
∴三棱锥O﹣PQR的体积为V=f(x)=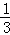
∴体积先增大,后减少,再增大,
故选:C
知识点
6.已知P是△ABC所在平面内一点,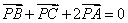
正确答案
解析
由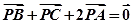
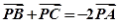

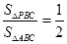
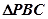
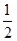
知识点
11.定义在R上的函数f(x)满足f(x)=
正确答案
﹣3
解析
由分段函数可知,当x>0时,f(x)=f(x﹣1)﹣f(x﹣2),
∴f(x+1)=f(x)﹣f(x﹣1)=f(x﹣1)﹣f(x﹣2)﹣f(x﹣1),
∴f(x+1)=﹣f(x﹣2),
即f(x+3)=﹣f(x),
∴f(x+6)=f(x),即当x>0时,函数的周期是6.
∴f(2013)=f(335×6+3)=f(3)=﹣f(0)=﹣log2(8﹣0)=﹣log28=﹣3,
故答案为:﹣3.
知识点
14.设动点





正确答案
解析
由题设可知,以


则有






显然







知识点
12.顶点在原点,经过圆

正确答案
解析
因为圆的圆心坐标为


知识点
13.如图,在△ABC中,O为BC中点,若AB=1,AC=3,<


正确答案
解析
如图所示,
根据题意,O为BC中点,
∴









=

∴|


知识点
15.若不等式|2x-1|+|x+2|≥a2+
正确答案
解析
|2x-1|+|x+2|=





知识点
17.已知


(1)求
(2)求

正确答案
(1)
(2)
解析
(1)∵△



∴


∴

(2)
所以周长为
=



所以周长最大值为
另解:由余弦定理可得:
又因为
所以:

知识点
19.某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(1)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
正确答案
见解析。
解析
(1)芯片甲为合格品的概率约为
芯片乙为合格品的概率约为
(2)(ⅰ)随机变量X的所有取值为90,45,30,-15




所以,随机变量X的分布列为:
(ⅱ)设生产的5件芯片乙中合格品n件,则次品有5﹣n件.
依题意,得 50n﹣10(5﹣n)≥140,解得 
设“生产5件芯片乙所获得的利润不少于140元”为事件A,
则 
知识点
20.给定椭圆






(1)求椭圆
(2)若直线




求
正确答案
见解析。
解析
(1)
(2)



知识点
16.已知数列
(1)求
(2)设



正确答案
见解析。
解析
(1)由
得
①—②得
即
因此,
由①,及

因此,

所以
(2)由(1)得


因为
所以当
当
综上,对任意正整数
知识点
18.如图,在三棱锥


(1)平面

(2)




正确答案
见解析。
解析
(1)在

经计算,得

因为




又因为



(2)取

因为
又因为平面

平面



所以

过



于是

因此,
又


由


即
所以
知识点
21.已知函数
(1)当


(2)若

(3)求证:
正确答案
见解析。
解析
(1)





(2) 因为
因为若

即

当
②当



③当

即方程
因为
所以方程
当



综合①②③知:
(3)(法一)根据(1)的结论,当


令




(法二)当




设当



根据(1)的结论,当


令

则有

因此,由数学归纳法可知不等式成立.