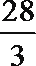- 真题试卷
- 模拟试卷
- 预测试卷
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.命题“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设集合






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在R上定义运算:对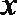
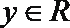
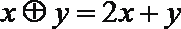

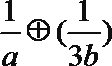
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如果方程

正确答案


解析
解析已在路上飞奔,马上就到!
知识点
9.不等式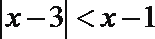
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数




正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.若对任意












(1)非负性:
(2)对称性:
(3)三角形不等式:
今给出三个二元函数,请选出所有能够成为关于

①
②
③
能够成为关于的

正确答案
①
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)求
(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数



(1)求函数
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x (x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)如果函数




(2)若函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数



(1)确定

(2)当

(3)证明:对任意

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)当

(2)令



正确答案
解析
解析已在路上飞奔,马上就到!