理科数学深圳市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

7．设函数上是单调递增函数，那么a的取值范围是（）

Ca<-1或a>1

Da>－2

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．曲线和直线y=1在y轴右侧的交点按横坐标从小到大依次记为P1，P2，P3，…，则|P2P4|为（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

1．设全集，集合，集合，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

2．已知，则的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

3. 已知，其中，则下列不等式成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．已知函数的导数，则函数的极值点的个数为（）

A1个

B2个

C3个

D4个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6. 在直线和之间，曲线与轴围成的图形的面积是（）

C2.5

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆的位置关系

题型：单选题

分值: 5分

8．已知向量=（1＋tanx，1－tanx），=（sin(x－)，sin(x＋),则与的关系为（）.

A夹角为锐角

B夹角为钝角

C垂直

D共线

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

9．在△ABC中，，则∠B=________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

10．已知是上的奇函数，当时，，则_________．

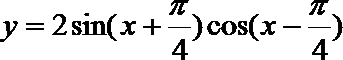
正确答案

-2

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

12．式子的值等于_____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

11．展开式中，只有第6项的系数最大，展开式中的常数项是________．

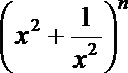
正确答案

252

解析

解析已在路上飞奔，马上就到！

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

分值: 5分

13．从1，3，5，7中任取2个数字，从0，2，4，6，8中任取2个数字组成没有重复数字的四位数，这样的四位数共有_________个.（用数字作答）．

正确答案

1296

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

14．一袋中装有4个白球，2个红球，现从袋中往外取球，每次取出一个，取出后记下球的颜色，然后放回，直到红球出现3次停止，设停止时,取球次数为随机变量,则 ________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

15.△ABC 中 A 为锐角,且．

（1）求的最大值；

（2）若，，，求 △ABC 的三个内角和 AC 边的长．

正确答案

（1）()；

（2） ,,

解析

解析已在路上飞奔，马上就到！

知识点

运用诱导公式化简求值二倍角的余弦正弦定理

题型：简答题

分值: 14分

17. 若，求函数的单调区间.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

16．已知A、B、C三点的坐标分别为、、

（1）若的值；

（2）若

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 14分

19.已知定义域为[0，1]的函数同时满足以下三条：

①对任意的[0，1]，总有；

②；

③若，，，则有成立。

解答下列各题：

（1）求的值；

（2）函数在区间[0，1]上是否同时适合①②③？并予以证明；

（3）假定存在[0，1]，使得[0，1]且，求证。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

18．一项“过关游戏”规则规定：在第n关要抛掷一颗骰子n次，如果这n次抛掷所出现的点数之和大于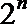，则算过关（假设骰子是均匀的正方体）。问：

（1）某人在这项游戏中最多能过几关？

（2）他连过前两关的概率是多少？

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：简答题

分值: 14分

20．已知f(x)是定义在[－1，1]上的奇函数。当a， b∈[－1，1]，且a+b≠0时，有成立。

（Ⅰ）判断函f(x)的的单调性，并证明；

（Ⅱ）若f(1)=1，且f(x)≤m2－2bm+1对所有x∈[－1，1]，b∈[－1，1]恒成立，求实数m的取值范围。

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷