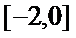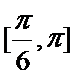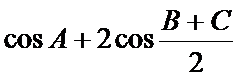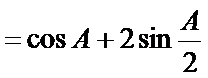- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.圆的极坐标方程为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“

正确答案
充分非必要
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
6.若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一盒中有


那么抽取次数

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
9.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知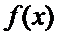
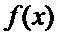
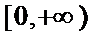
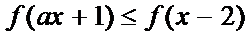
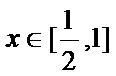
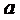
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数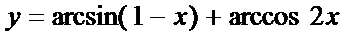
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.若点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数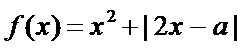
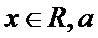
(1)若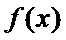
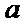
(2)设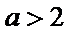
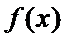
正确答案
(1)由已知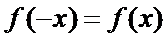
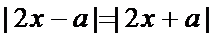
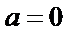
(2)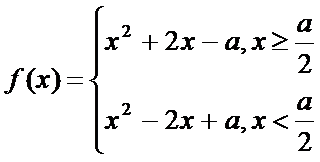
当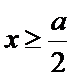
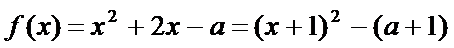
由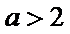
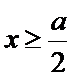
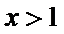
故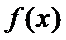
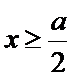
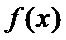
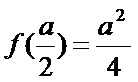
当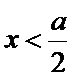
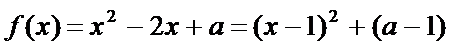
故当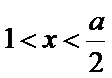
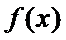
当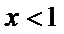
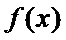
则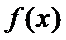
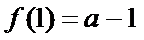
由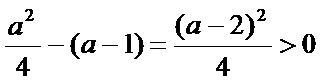
知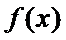
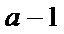
解析
解析已在路上飞奔,马上就到!
知识点
21.已知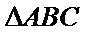
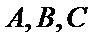
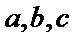
(1)若当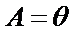
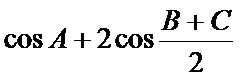

(2)设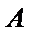
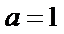
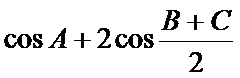
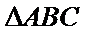
正确答案
(1)因为
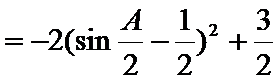
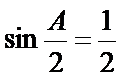
即三角形的内角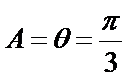
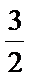
(2)由(1)结论可得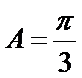
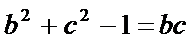
又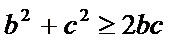

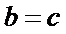
所以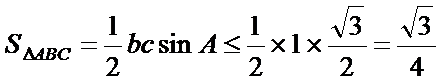
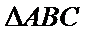

解析
解析已在路上飞奔,马上就到!
知识点
22.已知
(1)化简
(2)是否存在



正确答案
(1)

又因为
即
解得:定义域为

(2)若

所以

此时

即为存在的
解析
解析已在路上飞奔,马上就到!
知识点
24.已知函数




(1)判断函数

(2)若


(3)若定义域为









正确答案
解:(1)若



即


因此

若



即存在常数对


(2)


则
当

因此

则有
即
即
当


因此满足


(3) 函数



于是
即



因此
综上可知当


解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数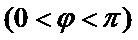
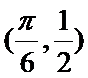
(1) 求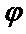
(2)将函数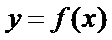
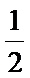
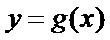
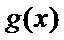
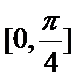
正确答案
(1)将已知函数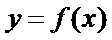
整理化简为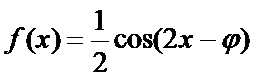
因其图象过点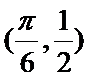
可得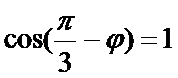
又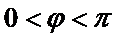
所以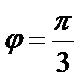
(2)由(1)知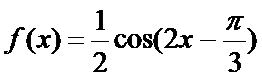
将函数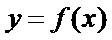
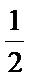
纵坐标不变,得到函数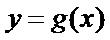
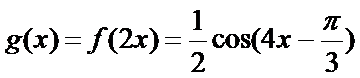
因为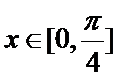
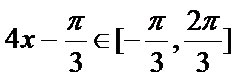
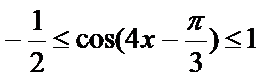
所以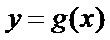
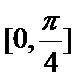
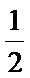
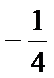
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数

(1)求实数

(2)若底数


(3)当


正确答案
(1)因为
所以对任意

即
化简得
又此方程有无穷多解,
必有
解得


(2)当


理由:设
因

于是,当
函数

(3)
所以根据(2),
当
函数



解得

若



所以必有



解析
解析已在路上飞奔,马上就到!