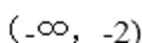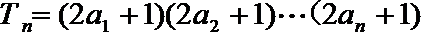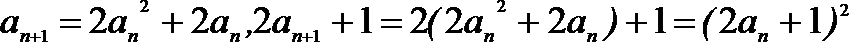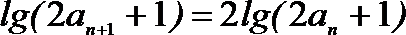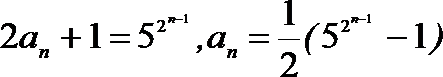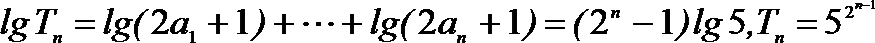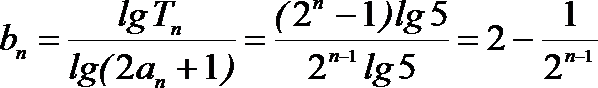- 真题试卷
- 模拟试卷
- 预测试卷
3.将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.两个圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在△ABC中,点P在BC上,且



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知实数x,y满足

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
12.函数
正确答案
(-1, 3)
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,设P,Q为△ABC内的两点,且

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知定义在闭区间[-3,3]上的两个函数:
正确答案
9≤k≤13
解析
解析已在路上飞奔,马上就到!
知识点
11.设集合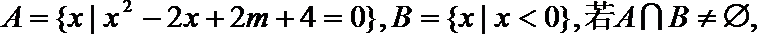
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在△ABC中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当
正确答案
(1)
则

且当

即

(2)当

当


所以


解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


正确答案





解析
解析已在路上飞奔,马上就到!
知识点
17.一个多面体的直观图(正视图,、侧视图,俯视图)如图所示,M,N分别为A1B,B1C1的中点,
(1)求证:MN//平面ACC1A1;
(2)求证:MN⊥平面AlBC;
(3)求二面角A—AlB—C的大小。
正确答案
由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CCl.
(1)
连结ACl,ABl.
由直三棱柱的性质得,AA⊥平面A1B1C1,
所以AA1⊥A1B1,则四边形ABB1A1为矩形.
由矩形性质得AB1过A1B的中点M.
在△AB1C1中,由中位线性质得MN//A Cl,
又AC1

所以MN//平面ACC1A1.
(2)
因为BC⊥平面ACClA1,AC
所以BC⊥ACl.
在正方形ACC1Al中,A1C⊥AC1.
又因为BC 
由MN//ACl,得MN⊥平面A1BC。
(3)由题意CB,CA,CC1两两垂直。故可以以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系。
又AC=BC=CC1=a,
则C(0,0,0),B(0,a,0),B1(0,a,a), A(a,0,0)C1(0,0,a)
则AB的中点E的坐标为(

又AC1⊥平面A1BC,故
设二面角A-A1B-C的大小为θ
则
由题意知,θ为锐角,所以θ=
解析
解析已在路上飞奔,马上就到!
知识点
20.定义:若数列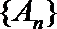
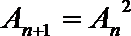

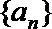
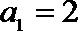
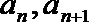
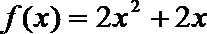
(1)证明数列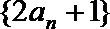
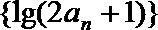
(2)设(1)中“平方递推数列”的前n项之积为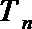
求数列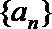

(3)记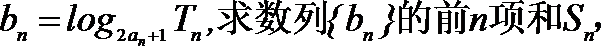
正确答案
(1)
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
19.设

(1)求椭圆的方程;
(2)求
(3)已知点A(8,0),B(2,0),是否存在过点A的直线l与椭圆交于不同的两点C,D,使得|BC|=|BD|?若存在,求直线的方程;若不存在,请说明理由.
正确答案
(1)由题设2a=8,2a+2c=12,则a=4,c=2,b2=12,
所以椭圆的方程是
(2)易知F1=(-2,0),F2(2,0)
设P(x,y),则
因为x∈[-4,4],所以x 2∈[0,16],8≤
点P为椭圆短轴端点时,
点P为椭圆长轴端点时,
(3)当直线l的斜率不存在时,直线l与椭圆无交点,所以若直线l存在,则直线l的斜率也存在,设直线l的斜率为k.则直线l的方程为y=k(x-8).
由方程组
则
设交点C(x1,y1)、D(x2,y2),CD的中点为T(x0,y0),
则
因为|BC|=|BD|,则BT⊥CD,
于是
所以不存在满足题目要求的直线l.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求h(x)的单调区间;
(2)若在y=h(x)在x∈(0,3]的图象上存在一点P(x0,y0),使得以P(x0,y0)为切点的切线的斜率k≥
(3)是否存在实数m,使得函数
正确答案
(1) 
于是,当x>a时,h’(x)>0,h(x)为增函数,
当0<x<a时,h’(x)<0,h(x)为减函数
所以h(x)的单调增区间是(a,+∞),单调减区间是(0,a)
(2)因为
所以在区间x∈(0,3]上存在一点P(x0,Y0),使得以P(x0,Y0)为切点的切线的斜率
即

因为
于是a≤

(3)若

即

构造函数

令
当x变化时F’(x)和F(x)的变化情况如下表:
所以当




解析
解析已在路上飞奔,马上就到!