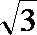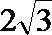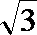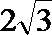理科数学三明市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1．若集合A＝{x|－2<x<1}，B＝{x|0<x<2}，则集合A∩B等于( )

A{x|0<x<1}

B{x|－2<x<1}

C{x|－2<x<2}

D{x|－1<x<1}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 5分

3．函数的实数解落在的区间是( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

5．定积分的值为( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

6．若，则＝( )

D－

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

9．已知是腰长为2的等腰直角三角形，点是斜边上任意一点，则的值是( )

D与点P的位置有关

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：单选题

分值: 5分

10.若函数的导函数在区间上的图象关于直线对称，则函数在区间上的图象可能是( )

A①②

B③④

C①③

D②④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

2．下列函数与有相同图象的一个函数是( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

4．已知A为三角形的内角，则的( )

A充分不必要条件

B必要不充分条件

C充要条件数

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定同角三角函数间的基本关系

题型：单选题

分值: 5分

7．若函数与在(0，＋∞)上都是减函数，则在(0，＋∞)上是( )

A增函数

B减函数

C先增后减

D先减后增

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

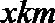
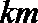
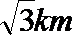
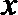
8. 某人向正东方向走后，向右转150°，然后朝新方向走3，结果他离出发点恰好是，那么的值为( )

C或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理

填空题本大题共5小题，每小题4分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 4分

11．已知α为第四象限的角，且= ________ .

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 4分

15．已知向量，||=1. 则函数y=+++…+的最大值为 ________ .

正确答案

284

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 4分

12．函数的定义域是 ________ ．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法

题型：填空题

分值: 4分

13. 已知，则= ________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

14．已知函数，其中．且的值域是［－，2］，则的取值范围是 ________ .

正确答案

(0,4］

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 13分

16．已知平面上三个向量、、的模均为1，它们相互之间的夹角均为120°.

（1）求证：-；

（2）若＞1 ，求的取值范围。

正确答案

（1）证明 ∵-,

∴-.

（2）解＞1＞1.

∵||=||=1，且、的夹角均为120°,

∴==1，·=-，

∴+1-＞1，即-＞0，

∴＞１或＜0.

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 13分

17.已知函数，.

（1）当时,求的单调区间与最值；

（2）若在定义域R内单调递增，求的取值范围。

正确答案

（1）当时，，∴.

令，即，解得：；

∴在时取得极小值，亦为最小值，即．

∴当时，函数的单调增区间是，递减区间为

的最小值为:

（2）∵，

∴.

∵在R上单调递增，

∴恒成立，

即，恒成立．

∵时，，∴.

即的取值范围为．

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法

题型：简答题

分值: 13分

19.△ABC的三个内角A，B，C所对的边分别为，，，向量，，且.

（1）求A的大小；

（2）现给出下列三个条件：①；②；③.试从中再选择两个条件以确定△ABC，求出你所确定的△ABC的面积。

正确答案

（1），

∴

，

，所以

（2）方案一：选择①③可确定△ABC。

由余弦定理

整理得

方案二：选择①②可确定△ABC。

又

由正弦定理得

（注：选择②③不能确定三角形）

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 14分

20．如图，有一个以圆心角为，半径为的扇形湖面．现欲在弧上任取一点，作扇形的内接矩形，使点在半径上，点在半径上，将该扇形湖面内隔为四个养殖区域。设矩形区域的面积为；

（1）当时，求矩形的面积；

（2）设，将表示成的函数关系式，并求出的最大值。

‍

正确答案

（1）当时,因为,

∴ ，，

又,

∴，

所以矩形的面积.

（2）因为，，，

所以

∴，即，

∴，

所以.

注：在△OPQ中，由正弦定理也可求出

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 14分

21．已知函数在点的切线方程为.

（1）求函数的解析式；

（2）设，求证：在上恒成立；

（3）已知，求证：。

正确答案

（1）将代入切线方程得

∴，化简得

又

∴ 解得：.

∴ .

（2）由已知得在上恒成立，化简得

即在上恒成立

设,则,

∴,,即

∴在上单调递增,

∴=0

∴在上恒成立.

（3） ∴

由(2)知,有

整理得

∴当时，.

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 13分

18．函数(，，)的一段图象如图所示．

（1）求函数的解析式；

（2）将函数的图象向右平移个单位，得到的图象，求函数的图象的对称轴和对称中心。

正确答案

（1）由题图知A＝2，，于是，

将的图象向左平移个单位长度，得的图象．

于是，

∴.

（2）依题意得.

故.

由,得.

∴的对称轴为, 对称中心为

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷