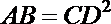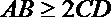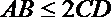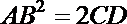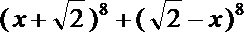- 真题试卷
- 模拟试卷
- 预测试卷
1.集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.6个完全相同的小球放在标有1、2、3、4号四个不同的盒子里,使每个盒子都不空的放法有( )种.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列函数中,既是奇函数又是周期为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.不等式组
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,曲线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.直角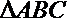
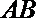
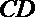
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,正四棱柱








(1)求证:



(2)求平面

正确答案
解:
(法一)
(1)证:











(2)延长







由正四棱柱




由







所以平面


(法二)
以






间直角坐标系,则



(1)






(2)设面


由




所以平面


解析
解析已在路上飞奔,马上就到!
知识点
18.甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要
面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设
每人面试合格的概率都是
(1)至少有1人面试合格的概率;
(2)签约人数
正确答案
解:
用


由题意知



(1)至少有1人面试合格的概率是
(2)




所以,


解析
解析已在路上飞奔,马上就到!
知识点
17.函数
(1)求实数
(2)求
正确答案
解:
(1)



(2)当

由




当

由



解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)设

(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆




(1)求椭圆
(2)已知直线






的最大值.
正确答案
解:
解析
解析已在路上飞奔,马上就到!
知识点
22.函数

(1)若函数

(2)若对



(3)设





正确答案
解:
(1)


或



即



所以,



综上,所求

(2)由题意,


解得

(3)由(1)知,当




因此,













因

①若


此时
②若



只需



综上,所求实数

解析
解析已在路上飞奔,马上就到!
知识点
16.过抛物线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若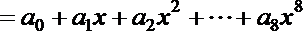
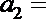
正确答案
448
解析
解析已在路上飞奔,马上就到!
知识点
13.不等式


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.倾斜角为


正确答案
解析
解析已在路上飞奔,马上就到!