- 真题试卷
- 模拟试卷
- 预测试卷
1．集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．下列判断错误的是（ ）
A“
B命题“
C在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高
D若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．从5位男实习教师和4位女实习教师中选出3位教师派到3个班实习班主任工作，每班派一名，要求这3位实习教师中男女都要有，则不同的选派方案共有（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．设函数
A
B2
C4
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于（ ）
A6
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．若直线2ax－by+2=0 （a >0, b>0） 被圆x2+y2+2x－4y+1=0截得的弦长为4，则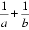
A
B
C2
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．当0<x<
A2
B2
C4
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知
A4
B4+4
C-4
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知函数f（x）＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．由函数
A4
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知函数f （x） = ax2+bx-1 （a , b∈R且a＞0 ）有两个零点，其中一个零点在区间（1，2）内，则a-b的取值范围为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．阅读下面的程序框图，则输出的s=_________．
正确答案
30
解析
解析已在路上飞奔，马上就到！
知识点
13．在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．设
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
16．正三棱锥P－ABC高为2，侧棱与底面所成角为45°，则点A到侧面PBC的距离是_________．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．甲乙两个学校高三年级分别有1100人，1000人，为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况，采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
乙校：
（Ⅰ）计算x，y的值。
（Ⅱ）若规定考试成绩在[120,150]内为优秀，请分别估计两个学校数学成绩的优秀率；
（Ⅲ）由以上统计数据填写下面2×2列联表，并判断是否有97．5%的把握认为两个学校的数学成绩有差异。
附：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．已知数列an的前n项和为Sn，且
点
（Ⅰ） 求数列an，bn的通项公式an和bn；
（Ⅱ） 设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．如图，在四棱锥P－ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB＝2，∠BAD＝60°．
（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）若PA＝AB，求PB与AC所成角的余弦值；
（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（Ⅰ）求函数
（Ⅱ）设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．选考题：请在下列A、B、C三题中任选一题作答
A．【选修4-1:几何证明选讲】
如图，Δ
（I） 求证：Δ
（Ⅱ）若
B．【选修4—4：坐标系与参数方程】
以直角坐标系的原点O为极点，x轴的正半轴为极轴，已知点P的直角坐标为
（I） 写出直线l的参数方程和圆C的极坐标方程；
（Ⅱ）试判定直线l和圆C的位置关系。
C．【选修4—5：不等式选讲】
设函数
正确答案
A.
B.
C.
解析
解析已在路上飞奔，马上就到！
知识点
21．已知椭圆C的中心在原点，焦点在x轴上，离心率等于
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）过椭圆C的右焦点
正确答案
解析
解析已在路上飞奔，马上就到！