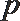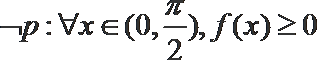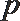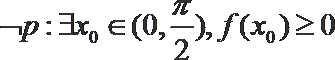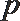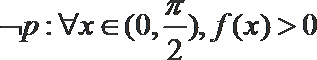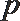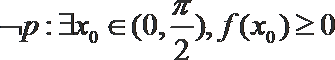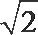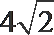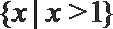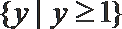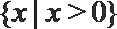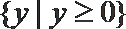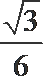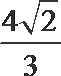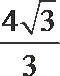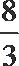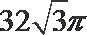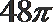- 真题试卷
- 模拟试卷
- 预测试卷
3.执行如图所示的程序框图,若输入x=3,则输出y的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知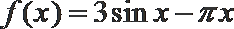
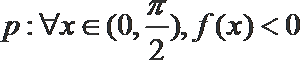
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.等轴双曲线
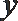

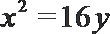
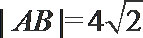

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 若集合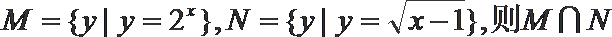
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.袋中有6个小球,分别标有数字1,2,3,4,5,6,甲乙两人玩游戏,先由甲从袋中任意摸出一个小球,记下号码


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图,一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形,则其体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 点A、B、C、D均在同一球面上,其中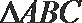
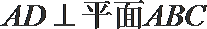
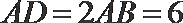
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 求形如




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知公比不为1的等比数列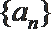
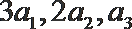

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.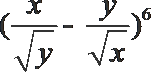
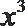
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
15.设实数



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.将6位志愿者分成4组,其中有2个组各2人,另两个组各1人,分赴2012年伦敦奥运会的四个不同场馆服务,不同的分配方案有___________种.(用数字作答)
正确答案
1080
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆








(2)平面上的点






正确答案
(I)由
设







消去



故椭圆

(II)由


因为




设
设
因为

解得

故所求直线


解析
解析已在路上飞奔,马上就到!
知识点
18. 在四棱锥




(1)求证:面

(2)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知
(1)求
(2)在△ABC中,a,b,c,分别是A,B,C的对边,若

正确答案
(1)
单调递增区间为:
解得:
故单调递增区间为:
(2)由正弦定理得:



又


解析
解析已在路上飞奔,马上就到!
知识点
19. 某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组
①[0,30),②[30,60),③[60,90),④[90,120),
⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240),
得到频率分布直方图如下.已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人;
(1)求n的值并补全下列频率分布直方图;
(2)如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的n名学生,完成下列2×2列联表:
是否有95%的把握认为学生利用时间是否充分与走读、住宿有关?
参考公式:
参考列表:
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因,记抽到“有效学习时间少于60分钟”的学生人数为X,求X的分布列及期望;
正确答案
(1)设第i组的频率为Pi(i=1,2,…,8),
则由图可知:P1=×30=,P2=×30=
∴学习时间少于60钟的频率为:P1+P2= 由题n×=5 ∴n=100
又P3=×30=, P5=×30=, P6=×30=, P7=×30=, P8=×30=,
∴P4=1-(P1+P2+P3+P5+P6+P7+P8)=1-=1-=
第④组的高度h=×==
频率分布直方图如图:(未标明高度1/120扣1分)
(2)
K2=≈5.556
由于K2>3.841,所以有95%的把握认为
学生利用时间是否充分与走读、住宿
有关
(3)由(1)知:第①组1人,
第②组4人,第⑦组15人,第⑧组10人,总计20人。则X的所有可能取值为0,1,2,3
P(X=i)=(i=0,1,2,3)
∴P(X=0)= ==, P(X=1)= ===, P(X=2)= ===, P(X=3)= ===
∴X的分布列为:
EX=0×+1×+2×+3×===
(或由X服从20,5,3的超几何分布,∴EX=3×=)
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)讨论函数
(2)当


(3)证明:
正确答案
(1)
当


当


当0<


则当



故


(2)因为
当

令

因为


且当



所以



故
(3)由(2)知当




令

所以


相加得
而
所以
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
22. 选修4-1:几何证明选讲
如图,A,B,C,D四点在同一个圆上,BC与AD的延长线交于点E,点F在BA的延长线上。
(1)若

(2)若

23. 选修4—4:坐标系与参数方程。
在平面直角坐标系中,曲线










(1)求曲线

(2)


24. 选修 4- 5 :不等式选讲
已知函数
(1)若

(2)解不等式
正确答案
22.
23.
24.选修4—5:不等式选讲
(1)
又当

∴
∴若使f(x)≤a恒成立,应有a≥fmax(x),即a≥3
∴a的取值范围是:[3,+∞)
(2)当

当

当

综合上述,不等式的解集为:
解析
解析已在路上飞奔,马上就到!