- 真题试卷
- 模拟试卷
- 预测试卷
4.设随机变量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
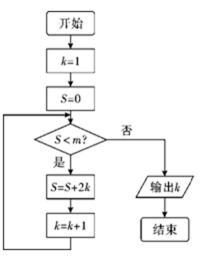
5.执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如图,






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知实数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设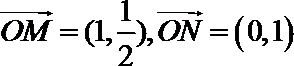
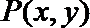
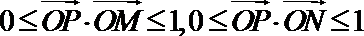
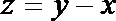
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在极坐标系中,若等边三角形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数f(x)=|lnx|,若0<a<b,f(a)=f(b),则a+2b的取值范围是____________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出定义:若


①函数


②函数

③函数

④函数

其中正确命题的序号是____________。
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,


(Ⅰ)判断△ABC的形状;
(Ⅱ)若

正确答案
(Ⅰ)解:由
∴





∴
∴
(Ⅱ)∵ 
∴
∴
而
∴

解析
解析已在路上飞奔,马上就到!
知识点
18.如图, 








(Ⅰ)求证:

(Ⅱ)求二面角
(Ⅲ)设点




正确答案
(Ⅰ)证明: 因为


因为



(Ⅱ)解:
因为

因为



所以



则




所以

设平面


即

因为




所以
所以二面角
(Ⅲ)解:点

设
因为


即

此时,点


解析
解析已在路上飞奔,马上就到!
知识点
17.为备战今年伦敦奥运会,射击队运动员们正在积极备战. 若某运动员每次射击成绩为10环的概率为
(1)至少有3次射击成绩为10环的概率;
(2)记“射击成绩为10环的次数”为


正确答案
解:设随机变量

(1)在5次射击中,至少有3次射击成绩为10环的概率为:


(2)
因为

解析
解析已在路上飞奔,马上就到!
知识点
19.已知圆













(Ⅰ)若


(Ⅱ)若动圆





正确答案
解:(Ⅰ)
∴点

又



∴
∴点

∴G的轨迹方程是
(Ⅱ)解:不存在这样一组正实数,由题意,若存在这样的一组正实数,
当直线



设

则

注意到


又点



因为弦




所以所求这组正实数不存在.
当直线

则此时


综上,所求的这组正实数不存在.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知





(Ⅰ)求证:数列
(Ⅱ)当n取何值时,
(Ⅲ)若


正确答案
解:(Ⅰ)∵


∴

又



∵
∴


(Ⅱ)由(I)可知


∴



当n<7时,



∴当n=7或n=8时,

(Ⅲ)由
依题意(*)式对任意
①当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由


而当m是偶数时
③当t>0时,由

∴

设
∵

∴
∴


所以实数的取值范围是
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若


(Ⅱ)若


正确答案
解:(Ⅰ)
①当


得


②当


得

综合①,②得b的取值范围是
(Ⅱ)令
当


∵


∴

当


∴

又因为函数

∴
∵


则

当a≥3时,
∴g(x)=0在
当

∴g(x)=0在
解析
解析已在路上飞奔,马上就到!