- 真题试卷
- 模拟试卷
- 预测试卷
3.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设偶函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.球面上三点A、B、C,其中AB为球的直径,若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.把函数


正确答案
y=sin4x
解析
解析已在路上飞奔,马上就到!
知识点
15.过点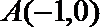
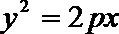
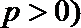
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在棱长为1的正方体ABCD-A1B1C1D1中,若点P为△BCD的重心,则D1P与平面ADD1A1所成角的大小为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在由正数组成的数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在△ABC中,



(1)求角A;
(2)若BC



正确答案
解:(1)由


(2)
同理:

故
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥P—ABCD中,底面ABCD为正方形,PD
(1)求证:EF
(2)求异面直线PD与AE所成的角的大小;
(3)求二面角F—PC—B的大小。
正确答案
解:(1)连结FO,





又


连结FB,可求得FB=PF=

又



(2)连结BD,


且EO



在Rt△EOA中,AO=
所以:异面直线PD与AE所成的角的大小为
(3)取PC的中点G,连结EG,FG,则EG是FG在平面PBC内的射影














所以
在Rt△FEG中,EG=

解析
解析已在路上飞奔,马上就到!
知识点
19.A、B是治疗同一种疾病的两种药,用若干试验进行对比试验,每个试验由4只小白鼠组成,其中2只服用A,另两只服用B,然后观察疗效,若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组,设每只小白鼠服用A有效的概率为

(1)求一个试验组为甲类组的概率;
(2)观察3个试验组,用

正确答案
解:(Ⅰ)设A1表示事件“一个试验组中,服用A有效的小白鼠有i只”,i= 0,1,2,
B1表示事件“一个试验组中,服用B有效的小白鼠有i只”,i= 0,1,2,依题意有
所求的概率为P = P(B0·A1)+ P(B0·A2)+ P(B1·A2=
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,
ξ的分布列为
数学期望
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆




(1)求椭圆的方程;
(2)已知定点



正确答案
解:(1)直线AB:



由①得
由②3得

(2)
Δ
设


则
∴


∴当

解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列







(1)求证:数列
(2)求证:数列
(3)求数列


正确答案
解:(1)∵
∴当

∴数列
(2)∵
∴
∵
∴

又∴


∴数列


(3)由(2)得
又∵
∴
∴
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数

(1)若


(2)如果

(3)是否存在最小的正整数


正确答案
解:(1)由题意知,





当



所以当



所以
(2)由题意

即

设


(3)对于函数
则
所以函数


即


显然,存在最小的正整数N=1,使得当

解析
解析已在路上飞奔,马上就到!