- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.记函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知

①若

②若


③若

④若

其中真命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知“命题


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.定义行列式运算:




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设集合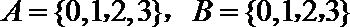
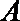
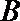
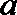
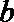
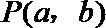

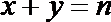

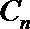

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




若两正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.称




①
②
③对任意的
则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在0, 1,2,3,4,5这六个数字所组成的没有重复数字的三位数中,其各个数字之和为9的三位数共有_________个(用数字做答)
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
15.已知:对于给定的






①对于


②对于给定的


若当且仅当







正确答案
4 , (5,1,3)
解析
解析已在路上飞奔,马上就到!
知识点
11.若
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
14.已知
从散点图分析,



正确答案
2.6
解析
解析已在路上飞奔,马上就到!
知识点
13.若不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 如图,在三棱锥P-ABC中, PA=3,AC=AB=4,PB=PC=BC=5,D.E分别是BC、AC的中点,F为PC上的一点,且PF:FC=3:1.
(1)求证:PA⊥BC;
(2)试在PC上确定一点G,使平面ABG∥平面DEF;
(3)在满足(2)的情况下,求二面角G-AB-C的平面角的正切值.
正确答案
解:(1)在△PAC中,∵PA=3,AC=4,PC=5,
∴
又AB=4,PB=5,∴在△PAB中,
同理可得
∵
∵
(2)
如图所示取PC的中点G,
连结AG,BG,
∵PF:FC=3:1,∴F为GC的中点
又D、E分别为BC、AC的中点,
∴AG∥EF,BG∥FD,又AG∩GB=G,EF∩FD=F,
∴面ABG∥面DEF.
即PC上的中点G为所求的点.
(3)由(2)知G这PC的中点,连结GE,
∴GE⊥平面ABC,过E作EH⊥AB于H,连结GH,则GH⊥AB
∴∠EHG为二面角G-AB-C的平面角.
∵
∴
∴
∴二面角G-AB-C的平面角的正切值为
解析
解析已在路上飞奔,马上就到!
知识点
21.设单调递增函数



(1)一个各项均为正数的数列




(2)在(1)的条件下,是否存在正数M使下列不等式:

正确答案
(1)



又

又


当




当





(2)假设
即

令

故





解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(I)求函数
(II)若

正确答案
解:(I)∵
即

又
又其图象上相邻对称轴之间的距离为π

(II)∵原式
又
即
解析
解析已在路上飞奔,马上就到!
知识点
20.在四边形





(Ⅰ )求点
(Ⅱ )若点










(Ⅲ)在(Ⅱ)的条件下,直线
正确答案
(Ⅰ)如图,设点

则



∴所求的轨迹
(解法一)
(Ⅱ)对函数

设切点坐标为
该切线方程是
又设点





化简,得
设


则



因此,当





(Ⅲ) 



又











(解法二)
(Ⅱ)设点
利用切点弦直线方程的结论可得出直线
即
由



因此,当





(Ⅲ) 由(Ⅱ)得知直线


后面解法同解法一.
解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)讨论

(2)求证:在(1)的条件下,
(3)是否存在实数


正确答案
(1)
∴当


当


∴
(2)


∴ 
令

当



∴
∴在(1)的条件下,
(3)假设存在实数


① 当




所以,此时
②当





③ 当




所以,此时
综上,存在实数


解析
解析已在路上飞奔,马上就到!
知识点
18.一个口袋中装有2个白球和


(1)试用含
(2)若
(3)记三次摸球恰有一次中奖的概率为


正确答案
解:(1)∵一次摸球从

任何一个球被选出都是等可能的,其中两球颜色相同有
∴一次摸球中奖的概率
(2)若

三次摸球是独立重复试验,三次摸球恰有一次中奖的概率是

(3)设一次摸球中奖的概率为
则三次摸球恰有一次中奖的概率为

∵
∴


∴当

∵


故当
解析
解析已在路上飞奔,马上就到!

















































































