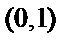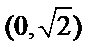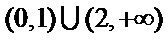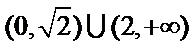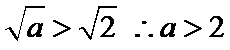- 真题试卷
- 模拟试卷
- 预测试卷
1.已知
正确答案
解析
因为

考查方向
解题思路
本题属于简单题,可使用直接法,(1)确定


易错点
计算过程易忽略
知识点
3.已知



正确答案
解析

考查方向
解题思路
【解题思路】本题属于简单题,可使用直接法,
易错点
注意公式
知识点
5.已知实数





正确答案
解析
画出可行域如图
如图可知在C

考查方向
解题思路
该题属于常规题1、画出可行域,注意a的取值2、找出最优解点,并求出点的坐标(含a)3、带入计算
易错点
主要易错于对简单线性规划问题不理解
知识点
6.设



正确答案
解析
以
∴
∴
考查方向
解题思路
该题属于常规题1、把

易错点
主要易错不能有效理解BCD的关系
知识点
8.函数
正确答案
解析
∵函数


∵在(0,0.5)上函数


∵函数

考查方向
解题思路
该题是由解析式得图像问题,使用排除法1、根据函数


易错点
本题易错在函数奇偶性的判断错误,特殊点位置判断错误
知识点
9. 执行如图所示的程序框图,那么输出的
正确答案
解析
易发现S结果以
又因为第2016退出循环,所以计算到2016

考查方向
解题思路
1、写出循环结构,找出S结果的规律2、根据周期性找出周期3、找出跳出循环的位置
易错点
本题易在判断上出错,导致提前或者延后跳出循环,第二没有发现S结果之间的规律,导致出错,
知识点
7. 函数

正确答案
解析
考查方向
解题思路
该题是常规题1、使用两角和与差的正弦公式
易错点
本题易错在
2.已知全集



正确答案
解析
使用集合交集的性质,借助数轴容易得出答案C。
考查方向
解题思路
本题属于简单题,可使用venn图直接观察得出
易错点
直接观察漏解
知识点
4. 函数
正确答案
解析
根据函数的性质
考查方向
解题思路
该题属于常规题,使用直接法
易错点
主要易错于常见初等函数的性质不熟
知识点
10. 已知函数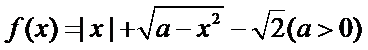
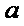
正确答案
解析
:
构造两个新函数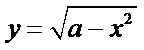
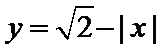
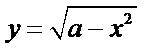
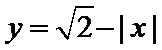
当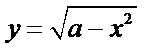
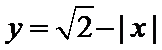
当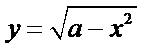
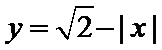
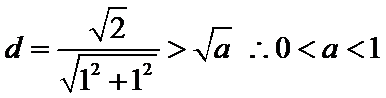
考查方向
解题思路
1、分离函数,构造两个新函数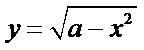
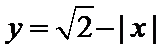
易错点
本题易错于不能有效构造新函数,不能画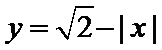
知识点
11.若“


正确答案
0
解析
根据函数性质
∴
考查方向
解题思路
1、求出
易错点
本题易错在恒成立问题的转化
知识点
14.圆锥被一个平面截去一部分,剩余部分再被另一个平面截去一部分 后,与半球(半径为
图和俯视图如图所示. 若
正确答案
解析
考查方向
易错点
主要出现在两个地方:①三视图还原直观图错误,②直观图读取直观图数据错误,特别是底面上的长宽数据
知识点
15.在平面直角坐标系







正确答案
解析
.
根据题意写出渐近线方程
所以
所以
考查方向
解题思路
该题思路比较清晰,主要有以下几个步骤1、求双曲线的渐近线2、根据圆的性质求出圆的方程3、渐近线与椭圆联立求出AB点坐标4、利用圆心到A的距离等于半径求出关系式
易错点
本题易错点主要集中在,1、渐近线的表达,2、外接圆的几何性质
知识点
12.若函数


正确答案
0或2
解析
∵
考查方向
解题思路
1、使用绝对值不等式
易错点
本题易错在使用三角不等式漏解,分类讨论忽略a的取值
知识点
13.从



正确答案
44
解析
根据题意如表分类
合计:4+12+12+16=44
考查方向
解题思路
1、根据题意划分类标准2、计算每种情况对应的结果
易错点
本题易错在分类考虑不全,或者分类错误
知识点
一次测试中,为了了解学生的学习情况,从中抽取了








18.求样本容量

19.在选取的样本中,从成绩是






正确答案
见解析
解析
考查方向
解题思路
本题的解题思路1、根据小矩形面积之和等于1,结合茎叶图,利用频数和频率之间的关系计算x,。2、分数在



易错点
本题第一问忽略了频率与小矩形面积之间的关系。第二问主要是区分不清超几何分布与二项分布之间的区别
正确答案
见解析
解析
考查方向
解题思路
本题的解题思路1、根据小矩形面积之和等于1,结合茎叶图,利用频数和频率之间的关系计算x,。2、分数在



易错点
本题第一问忽略了频率与小矩形面积之间的关系。第二问主要是区分不清超几何分布与二项分布之间的区别
如图,在四棱柱








延长


20.证明:

21.求直线

正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点1、确定线面平行判定的方式:面//面→线//面2、由面//面→线//面3、根据已知条件建立坐标系,并标记所需点的坐标4、计算相应面的法向量,并求向量的夹角5、判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1、确定线面平行判定的方式:面//面→线//面
2、由面//面→线//面
3、根据已知条件建立坐标系,并标记所需点的坐标
4、计算相应面的法向量,并求向量的夹角
5、判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
数列




22.求数列
23.设





正确答案
见解析
解析
考查方向
解题思路
1、借助等比数列的通项推导方法找到递推公式
2、利用奇偶项分别写出通项公式
3、对bn使用分组转化发求前n项和
4、利用函数思想求数列的单调性并确定最值
易错点
本题易错点有以下几点1、奇偶项的讨论忽略公比2、对bn的求解使用了讨论奇偶项3,不能有效讨论数列单调性
正确答案
见解析
解析

考查方向
解题思路
1、借助等比数列的通项推导方法找到递推公式
2、利用奇偶项分别写出通项公式
3、对bn使用分组转化发求前n项和
4、利用函数思想求数列的单调性并确定最值
易错点
本题易错点有以下几点
1、奇偶项的讨论忽略公比
2、对bn的求解使用了讨论奇偶项
3、不能有效讨论数列单调性








16.求
17.求

正确答案
解析
考查方向
解题思路
该题解题思路如下1、利用余弦定理变式求出角B2、使用三角形面积公式直接就出面积3、使用正弦定理求出边长
易错点
该题紧扣概念,错误主要集中在细节
正确答案
解析
考查方向
解题思路
该题解题思路如下1、利用余弦定理变式求出角B2、使用三角形面积公式直接就出面积3、使用正弦定理求出边长
易错点
该题紧扣概念,错误主要集中在细节




24.求抛物线
25.已知点









26.在25的条件下,直线




正确答案
见解析
解析
考查方向
解题思路
1、利用交点确定抛物线的方程
2、利用抛物线切线求解方式确定切线方程并求解BE点,借助向量证明是定值
3、利用直线和圆锥曲线之间的关系,求出韦达定理,并求出面积
4、借助函数的奇偶性和单调性,分类讨论确定最值
易错点
本题主要有以下几个错误:
1、抛物线过p的切线方程无法确定斜率
2、不能有效表达面积
3、面积与函数的结合不容易得到
正确答案
见解析
解析
由点






由

由
可得


切线

在




考查方向
解题思路
1、利用交点确定抛物线的方程
2、利用抛物线切线求解方式确定切线方程并求解BE点,借助向量证明是定值
3、利用直线和圆锥曲线之间的关系,求出韦达定理,并求出面积
4、借助函数的奇偶性和单调性,分类讨论确定最值
易错点
本题主要有以下几个错误:1、抛物线过p的切线方程无法确定斜率2、不能有效表达面积3、面积与函数的结合不容易得到
正确答案
见解析
解析
由直线


由

由韦达定理,得
于是
令



当

当


当


所以,当


因为



当





综上,



考查方向
解题思路
1、利用交点确定抛物线的方程2、利用抛物线切线求解方式确定切线方程并求解BE点,借助向量证明是定值3、利用直线和圆锥曲线之间的关系,求出韦达定理,并求出面积4、借助函数的奇偶性和单调性,分类讨论确定最值
易错点
本题主要有以下几个错误:
1、抛物线过p的切线方程无法确定斜率
2、不能有效表达面积
3、面积与函数的结合不容易得到
已知函数

27.当

28.若函数

29.若存在




注:自然对数的底数
正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1、第一问借助导数求函数单调性
2、利用导数性质,研究导函数零点问题
3、根据极值点情况对参数进行验证,证明
4、把存在性问题转化为求最值问题
易错点
本题易错
1、零点的判断有遗漏不全,
2、分类不清
3、参数多,讨论不清
正确答案
见解析
解析
.
考查方向
解题思路
本题解题思路
1、第一问借助导数求函数单调性
2、利用导数性质,研究导函数零点问题
3、根据极值点情况对参数进行验证,证明
4、把存在性问题转化为求最值问题
易错点
本题易错
1、零点的判断有遗漏不全,
2、分类不清
3、参数多,讨论不清
正确答案
见解析
解析
.
考查方向
解题思路
本题解题思路
1、第一问借助导数求函数单调性
2、利用导数性质,研究导函数零点问题
3、根据极值点情况对参数进行验证,证明
4、把存在性问题转化为求最值问题
易错点
本题易错
1、零点的判断有遗漏不全,
2、分类不清
3、参数多,讨论不清