理科数学周口市2015年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3.设向量a,b满足|a+b|=，|a-b|=，则ab = （）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

向量的模平面向量数量积的运算

题型：单选题

分值: 5分

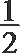
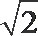
4.钝角三角形ABC的面积是，AB=1，BC= ，则AC=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

余弦定理

题型：单选题

分值: 5分

6.如图，网格纸上正方形小格的边长为1（表示1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

旋转体（圆柱、圆锥、圆台）简单空间图形的三视图

题型：单选题

分值: 5分

7.执行下图的程序框图，若输入的分别为1,2,3，则输出的=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

程序框图

题型：单选题

分值: 5分

9.已知函数，，若有两个不相等的实根，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数图象的应用函数零点的判断和求解

题型：单选题

分值: 5分

10.不等式组的解集记为.有下面四个命题：

：，

：,

：，

：.

其中真命题是（）

A，

B，

C，

D，

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用

题型：单选题

分值: 5分

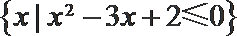
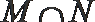
1.设集合M=｛0,1,2｝，N=，则=（）

A｛1｝

B｛2｝

C｛0，1｝

D｛1，2｝

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算一元二次不等式的解法

题型：单选题

分值: 5分

2.设复数，在复平面内的对应点关于虚轴对称，，则（）

A- 5

C- 4+ i

D- 4 - i

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数的基本概念复数代数形式的乘除运算

题型：单选题

分值: 5分

5.已知实数满足（），则下列关系式恒成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的单调性、奇偶性及其应用指数函数的单调性与特殊点对数函数的单调性与特殊点正弦函数的单调性

题型：单选题

分值: 5分

8.设等差数列的公差为d，若数列为递减数列，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

分值: 5分

11.已知，椭圆的方程为，双曲线的方程为，与的离心率之积为，则的渐近线方程为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程椭圆的几何性质双曲线的几何性质

题型：单选题

分值: 5分

12.设集合，那么集合A中满足条件“”的元素个数为（）

A60

B90

C120

D130

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

排列、组合的实际应用

填空题本大题共4小题，每小题5分，共20分。把答案填写在题中横线上。

题型：填空题

分值: 5分

14.三棱锥中，，分别为，的中点，记三棱锥的体积为，的体积为，则______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积

题型：填空题

分值: 5分

15.已知椭圆C：，点M与C的焦点不重合，若M关于C的焦点的对称点分别为A，B，线段MN的中点在C上，则______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质

题型：填空题

分值: 5分

16．若等比数列的各项均为正数，且，则_____。

正确答案

100

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质等比数列的性质及应用

题型：填空题

分值: 5分

13.正方形的四个顶点分别在抛物线和上，如图所示，若将一个质点随机投入正方形ABCD中，则质点落在阴影区域的概率是______.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分的简单应用与面积、体积有关的几何概型

简答题（综合题）本大题共70分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19.乒乓球台面被网分成甲、乙两部分，如图，甲上有两个不相交的区域，乙被划分为两个不相交的区域.某次测试要求队员接到落点在甲上的来球后向乙回球.规定：回球一次，落点在上记3分，在上记1分，其它情况记0分.对落点在上的来球，小明回球的落点在上的概率为，在上的概率为；对落点在上的来球，小明回球的落点在上的概率为，在上的概率为.假设共有两次来球且落在上各一次，小明的两次回球互不影响.求：

（Ⅰ）小明的两次回球的落点中恰有一次的落点在乙上的概率；

（Ⅱ）两次回球结束后，小明得分之和的分布列与数学期望.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

互斥事件、对立事件的概率离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 12分

17.在中，内角A，B，C的对边a，b，c，且，已知，，，求：

（1）a和c的值；

（2）的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的余弦函数三角形中的几何计算平面向量数量积的运算

题型：简答题

分值: 12分

18. 如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.

（Ⅰ）证明：PB∥平面AEC；

（Ⅱ）设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

题型：简答题

分值: 12分

20.已知椭圆的一个焦点为，离心率为，

（1）求椭圆C的标准方程；

（2）若动点为椭圆外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程直接法求轨迹方程

题型：简答题

分值: 12分

21.设函数（为常数，是自然对数的底数）.

（Ⅰ）当时，求函数的单调区间；

（Ⅱ）若函数在内存在两个极值点，求的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 10分

请从第22、23、24三题中任选一题作答。

22.选修4—1：几何证明选讲

如图，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB=CE

（Ⅰ ）证明：∠D=∠E；

（Ⅱ）设AD不是⊙O的直径，AD的中点为M，且MB=MC，证明：△ADE为等边三角形.

23.选修4—4：坐标系与参数方程

已知曲线：，直线：（为参数）.

（Ⅰ ）写出曲线的参数方程，直线的普通方程；

（Ⅱ）过曲线上任一点作与夹角为的直线，交于点，求的最大值与最小值.

24.选修4—5：不等式选讲

若，且.

（Ⅰ ）求的最小值；

（Ⅱ）是否存在，使得？并说明理由.

正确答案

22.

23.

24.

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷