- 真题试卷
- 模拟试卷
- 预测试卷
1.已知i为虚数单位,则复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若实数a≥0,b≥0,且ab=0,则称a与b互补,记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知某几何体的三视图如图所示,则该几何体的体积等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 某程序框图如图所示,若该程序运行后输出的值是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知各项均为正数的等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数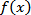
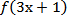
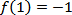
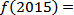
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.抛物线的顶点在原点,对称轴是x轴,抛物线上点(-5,m)到焦点距离是6,则抛物线的方程是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知双曲线中心在原点且一个焦点为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 
正确答案
1+ln2
解析
解析已在路上飞奔,马上就到!
知识点
14. 实数x,y,k满足




正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知公差不为0的等差数列



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16. 表面积为





正确答案
27
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列
(1)求数列
(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在三棱柱




(Ⅰ)求证:
(Ⅱ)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.乒乓球台面被球网分隔成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D.某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,在D上记1分,其他情况记0分.对落点在A上的来球,队员小明回球的落点在C上的概率为,在D上的概率为;对落点在B上的来球,小明回球的落点在C上的概率为,在D上的概率为.假设共有两次来球且落在A,B上各一次,小明的两次回球互不影响.求:
(1)小明两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和ξ的分布列与数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆
(1)若直线AP与BP的斜率之积为
(2)若|AP|=|OA|,证明直线OP的斜率k满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.选修4—1:几何证明选讲
如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.
(1)若
(2)若

23.选修4-4:坐标系与参数方程
在直角坐标系xoy中,以O为极点,x轴正半轴为极轴建立坐标系。圆



(1)求

(2)设P为




24.选修4-5:不等式选讲
设函数


(1)求M;
(2)当

正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)设

(2)设




正确答案

解析
解析已在路上飞奔,马上就到!















































