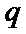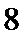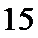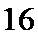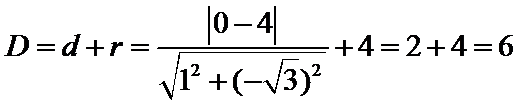- 真题试卷
- 模拟试卷
- 预测试卷
2.下列函数中,既是偶函数又存在零点的是( )
正确答案
解析
由选项可知,B,C项均不是偶函数,故排除B,C,A,D项是偶函数,但D项与x轴没有交点,即D项的函数不存在零点,故选A.
考查方向
解题思路
根据函数的奇偶性和函数零点的相关概念判断,结合选项依次判断。
易错点
函数的奇偶性理解错误,忽略函数零点的意义。
知识点
3.设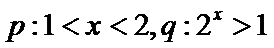


正确答案
解析
由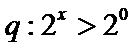
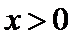
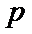
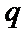
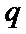
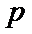

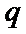
考查方向
解题思路
先利用指数函数的运算法则,然后判断是什么样的条件。
易错点
充分条件和必要条件混淆
知识点
4.下列双曲线中,焦点在

正确答案
解析
由题意,选项





考查方向
解题思路
根据选项逐一求解
易错点
计算错误,对渐近线方程形式记忆混淆
知识点
5.已知



正确答案
解析
由A选项,
















考查方向
解题思路
根据选项逐一进行判断
易错点
平面和直线的位置关系混淆,考虑问题不全面
知识点
7.一个四面体的三视图如图所示,则该四面体的表面积是( )
正确答案
解析
由题意,该四面体的直观图如下:



则


考查方向
解题思路
先根据三视图还原成直观图,然后根据立体几何相关性质求解。
易错点
立体感不强,三视图还原成直观图错误
知识点
10.已知函数




时,函数
正确答案
解析
由题意,











当


考查方向
解题思路
先根据给出的已知条件,求出三角函数的解析式,接着判断函数的最值。
易错点
三角函数的图象和性质掌握不好,综合能力弱
知识点
1.设i是虚数单位,则复数
正确答案
解析
由题意

考查方向
解题思路
先化简,再根据复数的几何意义做判断
易错点
复数的运算错误,复数的几何意义理解的不透彻
知识点
6.若样本数据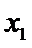
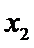
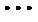
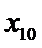


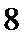
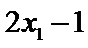
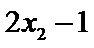
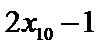
差为( )
正确答案
解析
设样本数据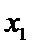
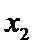
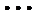
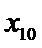
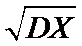
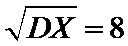
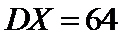
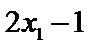
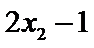
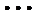
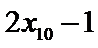
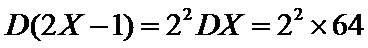
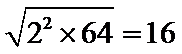
考查方向
解题思路
根据题意和相关公式分别求解。
易错点
样本的方差和标准差公式记忆错误,不理解题意
知识点
8.





结论正确的是( )
正确答案
解析
如图,
由题意,












考查方向
解题思路
先根据向量相关性质把有向线段用坐标的形式表示出来,然后利用垂直关系求得。
易错点
计算错误,向量的数量积表示错误
知识点
9.函数
正确答案
解析
由







考查方向
解题思路
先根据图像和函数相关性质、单调性、奇偶性、拐点等性质进行判断参数的符号。
易错点
数形结合思想掌握不好,函数相关性态求解有问题,
知识点
11. 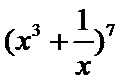
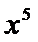
正确答案
解析
由题意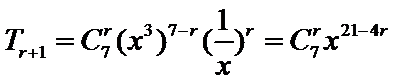

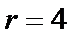
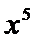
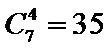
考查方向
解题思路
先利用公式展开,然后找到次数为5的项,进而求出系数。
易错点
二项式展开式公式记忆混淆,找系数时次数有遗漏项
知识点
12.在极坐标中,圆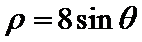

正确答案
解析
由题意可知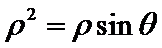

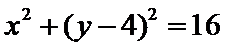
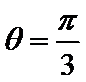
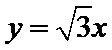
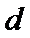
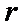
考查方向
解题思路
先将极坐标转换成直角坐标下的方程形式,然后利用点到熟悉的圆锥曲线的求距离的方法求解
易错点
极坐标转换成直角坐标失败,不会求点到线的距离
知识点
13.执行如图所示的程序框图(算法流程图),输出的
正确答案
解析
由题意,程序框图循环如下:①





考查方向
解题思路
根据顺序结构判断是否进入循环,判断循环输出,进而求出最后输出的数值。
易错点
流程图读不懂,在判断流程时出现错误
知识点
14.已知数列



正确答案
解析
由题意,









考查方向
解题思路
先根据一直条件求出等比数列的首项和公比,进而利用公式求前n项和。
易错点
等比数列及其前N项和求解错误,公式记忆不牢
知识点
15.设

是 .(写出所有正确条件的编号)
①




正确答案
①③④⑤
解析
令




















考查方向
易错点
函数和方程的关系找不出来,不会利用导数判断函数有无根的情况。
知识点
16.在




正确答案
解析
设



所以
又由正弦定理得
由题设知

在

考查方向
解题思路
设出






易错点
正弦定理、余弦定理运用错误,计算错误
知识点
设



19.求数列
20.记

正确答案
(1)
解析
(Ⅰ)解:



从而切线方程为



考查方向
解题思路
(Ⅰ)对题中所给曲线的解析式进行求导,得出曲线






易错点
求导错误,不会联系导数和曲线之间的关系。
正确答案
(2)
解析
(Ⅱ)证:由题设和(Ⅰ)中的计算结果知

当

当

所以
综上可得对任意的

考查方向
解题思路
(Ⅱ)要证










易错点
证明不等式成立时,找不到合理适当的放缩不等式
如图所示,在多面体






21.证明:
22.求二面角
正确答案
解析
(Ⅰ)证明:由正方形的性质可知














解题思路
(Ⅰ)证明:依据正方形的性质可知






易错点
找不到线面平行和线线平行的关系。
正确答案
(2)
解析
(Ⅱ)因为四边形














设面













考查方向
解题思路
因为四边形




















易错点
找不到二面角的平面角,计算能力弱.
已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
17.求第一次检测出的是次品且第二次检测出的是正品的概率
18.已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所
需要的检测费用(单位:元),求X的分布列和均值(数学期望)
正确答案
(1)
解析
(Ⅰ)记“第一次检查出的是次品且第二次检测出的是正品”为事件

解题思路
(Ⅰ)依据题目所给的条件可以先设“第一次检查出的是次品且第二次检测出的是正品”为事件

易错点
计算事件发生的概率错误
分布列表示不出来,求相应的概率时错误,不会求数学期望。
正确答案
(2)
解析
(Ⅱ)




故

考查方向
解题思路
(Ⅱ)



易错点
分布列表示不出来,求相应的概率时错误,不会求数学期望。
设椭圆






23.求E的离心率e;
24.设点C的坐标为

正确答案
(I)
解析
(Ⅰ)由题设条件知,点





考查方向
解题思路
(Ⅰ)由题设条件,可得点





易错点
椭圆方程相关性质、概念、公式记忆错误,计算能力弱
正确答案
解析
(Ⅱ)由题设条件和(Ⅰ)的计算结果可得,直线


















考查方向
1.椭圆的离心率;2.椭圆的标准方程;3.点点关于直线对称的应用.
解题思路
由题设条件和(Ⅰ)的计算结果知,直线

















易错点
圆锥曲线的相关性质、概念、公式记忆错误,计算能力弱
设函数
25.讨论函数

26.记


27.在(Ⅱ)中,取


正确答案
(Ⅰ)极小值为
解析
(Ⅰ)



因为

①当

②当

③当







因此,




考查方向
解题思路
(Ⅰ)将



求导得





















易错点
函数求导错误,分类讨论能力弱,计算能力弱
正确答案
解析
:
(Ⅱ)

当

当

由此可知,函数


考查方向
解题思路
当




易错点
绝对值不等式性质运用错误,计算错误,不会合理放缩不等式
正确答案
(Ⅲ)1.
解析
(Ⅲ)



取


由此可知,

考查方向
解题思路
(Ⅲ)当








易错点
平均值不等式的性质,计算能力弱