- 真题试卷
- 模拟试卷
- 预测试卷
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.锐角



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 将直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知直线


正确答案
2或-3
解析
解析已在路上飞奔,马上就到!
知识点
13.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 如图:



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
15.有以下四个命题:
①函数

②函数


③对于函数



④函数



⑤
其中正确的命题是_______(填上正确命题的序号)
正确答案
①②
解析
解析已在路上飞奔,马上就到!
知识点
14.在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 设


(I)求
(II)设





(Ⅲ)若
正确答案
(Ⅲ)
所以

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)求曲线

(2)求证:函数


正确答案
解:(1)函数

所以曲线

(2)
因为


所以方程


即

所以函数

由于

又
所以函数


解析
解析已在路上飞奔,马上就到!
知识点
19. 在平面四边形


(1)求证: 

(2)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量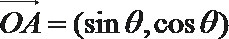
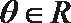
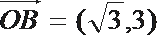
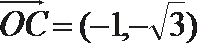
(1)若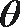
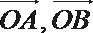
(2)若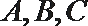
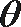
正确答案
解:(1)假设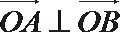
即
而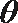
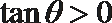
即若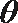
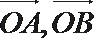
(2)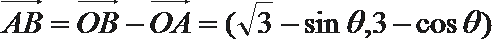
由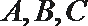
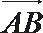
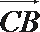
所以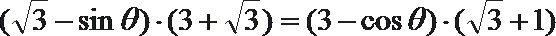
化简得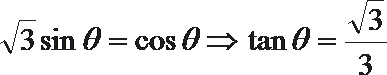
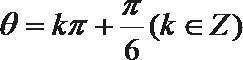
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)用五点作图法,作出函数
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知数列



(1)判断数列
(2)当






正确答案
解:(1)由已知
两式相减得
即

当

又

从而仅当


又


当


(2)由(1)知当
因为
从而
=

由上



当

当

当
又
所以

解析
解析已在路上飞奔,马上就到!