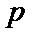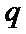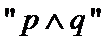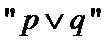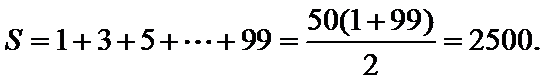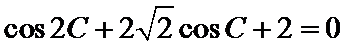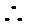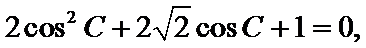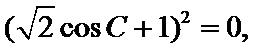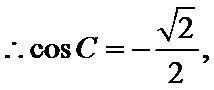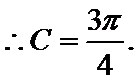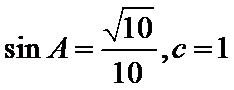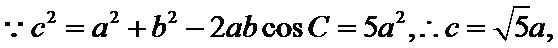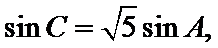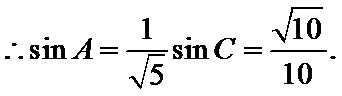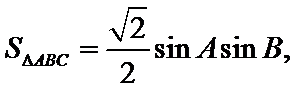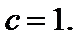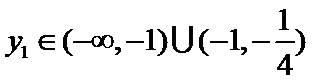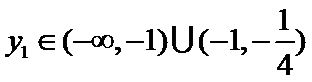- 真题试卷
- 模拟试卷
- 预测试卷
1.定义集合



正确答案
解析



考查方向
解题思路
1.先根据题中给出的新定义求出
易错点
1.不理解题中给出的新定义;2.记不住子集的个数是多少个导致出错(忘记空集)
知识点
2. 

正确答案
解析


考查方向
解题思路
1.先用复数的运算法则得到
易错点
1. 
知识点
4. 命题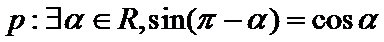
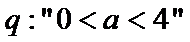
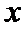
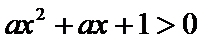
正确答案
解析
对于命题

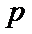
对于命题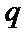


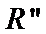
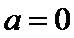
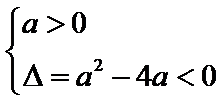
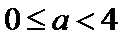
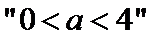
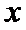
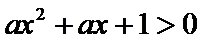
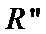
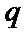
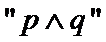
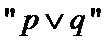
考查方向
解题思路
1.先判断命题p,q的真假;2.利用复合命题真假的判断方法判断即可。
易错点
1.不会判断命题p的真假;2.不知道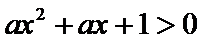
知识点
3.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( )
正确答案
解析
由题意得,甲班学生成绩的中位数为83,则


考查方向
解题思路
1.先根据甲班的中位数求出x=3;2.利用平均数求出
易错点
1.不会读取茎叶图中的信息;2.运算求解出错。
知识点
5. 已知变量





正确答案
解析
由约束条件表示的可行域如图所示,作直线l:ax+y=0,过点(1,1)作l的平行线l′,则直线l′介于直线x+2y-3=0与直线y=1之间,
因此,-<-a<0,即0<a<.
考查方向
解题思路
1.先作出可行域; 2. 作直线l:ax+y=0,过点(1,1)作l的平行线l′,则直线l′介于直线x+2y-3=0与直线y=1之间,即可得到答案。
易错点
1.可行域画错; 2.不会将题中给出的条件目标函数

知识点
6. 设


正确答案
解析
由

又
即

由不等式

考查方向
解题思路
1.先根据基本不等式转化题中给出的条件

易错点
1.看不出


知识点
7. 如图是函数



正确答案
解析
由图象可知A=1,T=-=π,∴ω==2.
∵图象过点,且在函数的单调递减区间上,
∴sin=0,∴
∴φ=+2kπ,k∈Z. ∴
故将函数
考查方向
解题思路
1.先根据图像求出


易错点
1.不会根据图像求解析式中的φ=+2kπ,k∈Z.2.在将
知识点
8. 某公司新招聘进8名员工,平均分给下属的甲、乙两个部门,其中两名英语翻译人员不能分给同一个部门;另三名电脑编程人员也不能分给同一个部门,则不同的分配方案种数是( )
正确答案
解析
由于均分8人,所以甲、乙两个部门各4人。完成这件事情分两类:第一类,甲部门有两名电脑编程人员,有

考查方向
解题思路
1.先根据甲部门有几名电脑编程人员分为两类;
2.然后分别求每一类由多少种不同的分配方案,然后相加即可。
易错点
1.不知道该如何进行分配导致混乱;
2.意识不到两个部门的人员组成是什么样的。
知识点
9. 如图,菱形





正确答案
解析
由平面向量的数量积的几何意义知,



考查方向
解题思路
1.先将所求的函数的最大值的情况找到;2.利用平面向量基本定理将
易错点
1.不知道
知识点
10.已知





正确答案
解析
设

所以
考查方向
解题思路
1.先将函数


易错点
1.不知道将函数

知识点
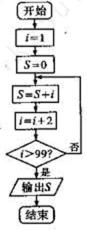
11.执行如图所示的程序框图,则输出的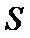
正确答案
2500
解析
考查方向
解题思路
根据程序框图发现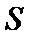
易错点
1.程序运行不完,导致求成前49项的和;2.不能发现是和等差数列的前n项和有关。
知识点
12. 已知在正方体




正确答案
解析
以








设直线



考查方向
解题思路
1.建立空间直角坐标系,写出所需各点的坐标;2.求平面


易错点
1.直线与平面所成的角的公式记错,导致求成
知识点
14.椭圆






正确答案
解析
不妨设双曲线










考查方向
解题思路
1.先求出双曲线的渐近线方程;2.根据





易错点
1.对于题中给出的条件
知识点
13.若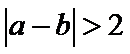
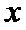
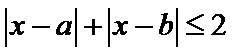
正确答案
解析
根据绝对值的意义,
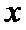
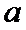

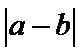
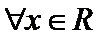

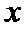
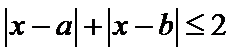
考查方向
解题思路
1.先根据绝对值的几何意义得到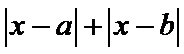
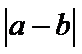
易错点
1.不会将题中要求的结构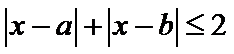
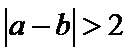
知识点
15.对于函数
设







某同学经过探究发现:任何一个三次函数


正确答案
2016
解析








设
则
两式相加得
考查方向
解题思路
1.先根据题中给出的信息求出
易错点
1.不理解题中给出的新概念拐点是什么导致无法入手;2.不会根据对称中心转化为倒序相加求和。
知识点
在
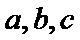
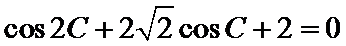
16.求角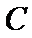
17.若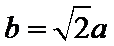
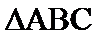

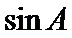

正确答案
(1) 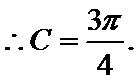
解析
(Ⅰ)
即
又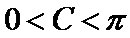
考查方向
解题思路
根据题中给出等式求出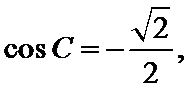
易错点
对于正弦定理的反复转化不明白。
正确答案
(2)
解析
(Ⅱ)
由正弦定理,得
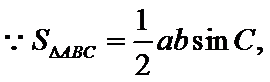
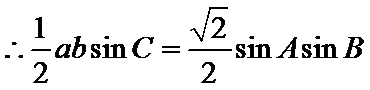
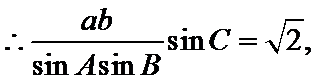
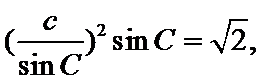
考查方向
解题思路
先根据余弦定理求出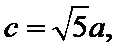
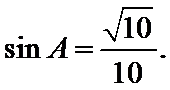
易错点
不知道该如何使用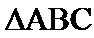
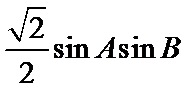
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=3,BC=2AB=2,E,F分别在BC,AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
20.若



使得
21.求三棱锥A-CDF的体积的最大值,并求此时二面角E-AC-F的余弦值.
正确答案
(1)
解析
(Ⅰ)因为平面



所以



所以
在折起过程中,


所以
以


若




可得平面

因为
所以
故
则

所以线段



考查方向
解题思路
先根据题中给出的条件证明

易错点
1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。
正确答案
(2)
解析
(Ⅱ)设


所以
所以当


可得



所以



设平面

则

取

设平面

则
同理可得
所以
所以二面角E﹣AC﹣F的余弦值为
考查方向
解题思路
设出变量后得到函数
易错点
1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。
2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为



18.求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
19.试求袁先生2016年上半年同时投资甲、乙两只股票的总收益的分布列和数学期望.
正确答案
(1)
解析
(Ⅰ)袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率为
考查方向
解题思路
直接根据题意求即可;
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
正确答案
((2)
解析
(Ⅱ)用

所以,

考查方向
解题思路
先设出随机变量后写出其取值,然后求其取各个值的概率列分布列带入期望公式即可。
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
已知数列






22.分别求数列

23.若



正确答案
(1)

解析
(Ⅰ)


又因为

设等比数列

由已知

解得


所以,
考查方向
解题思路
先利用已知数列的前n项和求通项公式求出

易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
正确答案
(2)
解析
(Ⅱ)
设数列





当
当


则

1-2得
所以
所以,
考查方向
解题思路
先由第(1)问得到
易错点
1.不会利用数列的前n项和求通项公式;2.对于数列
抛物线C的方程为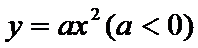
24.求抛物线C的焦点坐标和准线方程;
25.设直线AB上一点M,满足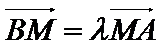
26.当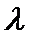
正确答案
(1)焦点坐标为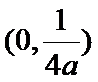
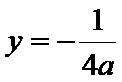
解析
(Ⅰ)由抛物线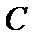
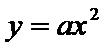
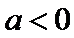
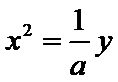
焦点坐标为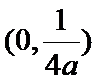
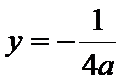
考查方向
解题思路
根据抛物线的几何性质直接得到即可;
易错点
无
正确答案
(2)略;
解析
(Ⅱ)证明:设直线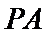
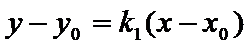
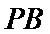
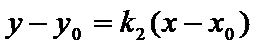
点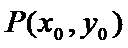
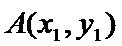
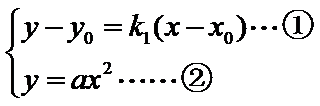
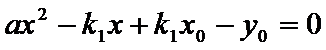
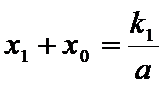
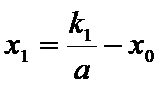
又点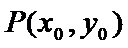
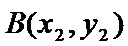
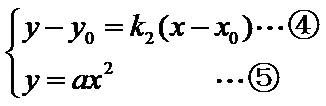
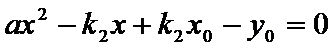
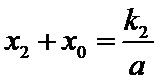
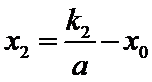
由已知得,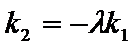
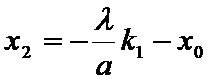
设点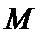
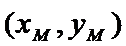
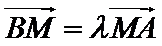
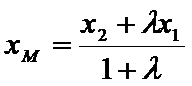
将③式和⑥式代入上式得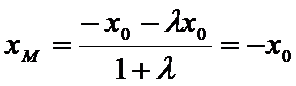
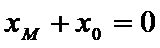
∴线段
考查方向
解题思路
1
先根据条件求出A,B的横坐标后带入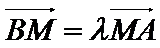
易错点
不会求解点A,B的坐标,运算量大;
正确答案
(3)
解析
(Ⅲ)因为点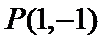
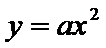
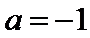
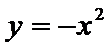
由③式知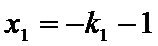
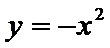
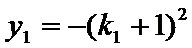
将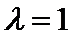
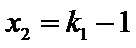
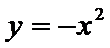
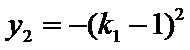
因此,直线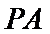
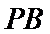
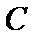
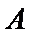
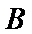
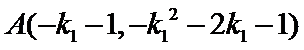
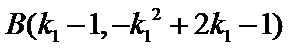
于是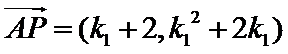
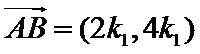
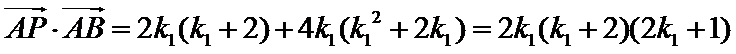
因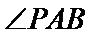
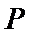
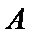
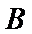
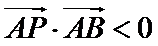
求得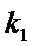
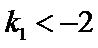
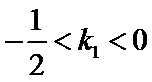
又点
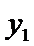
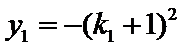
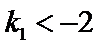
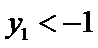
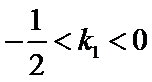
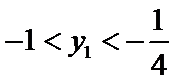
考查方向
解题思路
先求出抛物线的方程,然后根据第(2)问求出点A,B的坐标,然后将∠PAB为钝角转化为向量求解即可。
易错点
不会转化题中给出的条件∠PAB为钝角,导致做不出正确答案。
已知函数
27. 判断函数

28. 若

29.求证:
正确答案
(1)
解析
(Ⅰ)


考查方向
解题思路
直接求导后判断出
易错点
导后的函数不会变形为
正确答案
3;
解析
(Ⅱ)


令

又



当


∴

考查方向
解题思路
先分离参数后变为

易错点
无
正确答案
(3)略
解析
(Ⅲ)由(Ⅱ)知

令
∴
∴
考查方向
解题思路
根据第(2)问放缩
易错点
不会利用放缩法得到