- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.一个篮球运动员投篮一次得3分的概率为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.对于集合M、N,定义M-N={x|x∈M且x∉N},M⊕N=(M-N)∪(N-M),设A={y|y=3x, x∈R},B={y|y=-(x-1)2+2,x∈R},则A⊕B等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“所有能被2整除的整数都是偶数”的否定是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设f(x)=lg

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.对于任意两个正整数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数y=f(x)的周期为2,当x∈[-1,1]时f(x)=x2,那么函数y=f(x)的图象与函数y=|lgx|的图象的交点共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知集合A={x∈R| 

正确答案
由题意得:
A={x∈R|
B={x∈ R|x2-x+m-m2≤0}
={x∈ R|(x-m)(x-1+m)≤ 0}
由A∪ B=A知B⊆ A,
得-1<m≤2,-1<1-m≤2,
解得:-1<m<2.
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1) 求
(2) 若方程

正确答案
(1)因为
所以
即
∴
∴
∴
(2)依题意知:
∴ 由
得
∴ 
令

1)
2)*式有一正一负根,
3)两相等正根,

解析
解析已在路上飞奔,马上就到!
知识点
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
正确答案
(1)由题意:当0≤x≤20时,v(x)=60;
当20≤x≤200时,设v(x)=ax+b,
再由已知得200a+b=0,20a+b=60,
解得a=-

故函数v(x)的表达式为
(2)依题意并由(1)可得

当0≤x≤20时,f(x)为增函数,
故当x=20时,其最大值为60×20=1200;
当20≤x≤200时,


当且仅当x=200-x,即x=100时,等号成立.
所以,当x=100时,
f(x)在区间[20,200]上取得最大值
综上,当x=100时,
f(x)在区间[0,200]上取得最大值
即当车流密度为100辆/千米时 ,车流量可以达到最大,最大值约为3333辆/小时.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数f(x)=x2+4ax+2a+6.
(1)若函数f(x)的值域为[0,+∞),求a的值;
(2)若函数f(x)的函数值均为非负数,求f(a)=2-a|a+3|的值域.
正确答案
(1)∵ 函数的值域为[0,+∞),
∴ Δ=16a2-4(2a+6)=0,
∴ 2a2-a-3=0,
∴ a=-1或a=
(2)∵ 对一切x∈R函数值均为非负,
∴ Δ=8 (2a2-a -3)≤0,
∴-1≤a≤
∴ a+3>0,
∴ f (a)=2-a|a+3|=a2-3a+2=-
∵ 二次函数f(a)在
∴ 
即-
∴ f(a)的值域为[-
解析
解析已在路上飞奔,马上就到!
知识点
21.已知p:∀x∈R,2x>m(x2+1),q:∃x0∈R,x+2x0-m-1=0,且p∧q为真,求实数m的取值范围.
正确答案
2x>m(x2+1) 可化为mx2-2x+m<0.
若p:∀x∈ R, 2x>m(x2+1)为真,
则mx2-2x+m<0对任意的x∈ R恒成立.
当m=0时,不等式可化为-2x<0,
显然不恒成立;
当m≠0时,有m<0,Δ= 4-4m2<0,
∴ m<-1.
若q:∃x0∈ R,
则方程x2+2x-m-1=0有实根,
∴ Δ=4+4(m+1)≥0,∴ m ≥-2.
又p∧ q为真,故p、q 均为真命题.
∴ m<-1且m≥-2,
∴-2≤m<-1.
解析
解析已在路上飞奔,马上就到!
知识点
22.设函数f (θ)=sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为(
(2)若点P(x,y)为平面区域
正确答案
(1)由点P的坐标和三角函数的定义可得
sinθ=

于是f(θ)=

(2)作出平面区域Ω(即三角区域ABC),
其中A(1,0),B(1,1),C(0,1).
于是0≤θ≤
又f(θ)=

且


故当θ+


f(θ)取得最大值,且最大值等于2 ;
当θ+

f(θ)取得最小值,且最小值等于1.
解析
解析已在路上飞奔,马上就到!
知识点
13.已知集合A={(x,y)| 
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
14.若(a+1)

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.用二分法求方程x2=2的正实根的近似解(精确度0.001)时,如果我们选取初始区间是[1.4,1.5],则要达到精确度要求至少需要计算的次数是__________次.
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
16.下列结论中是真命题的是__________(填序号).
①f(x)=ax2+bx+c在[0,+∞)上是增函数的一个充分条件是
②已知甲:x+y≠3,乙:x≠1或y≠2,则甲是乙的充分不必要条件;
③数列{an}(n∈N*)是等差数列的充要条件是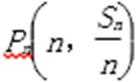
正确答案
②③
解析
解析已在路上飞奔,马上就到!
















































