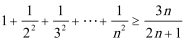- 真题试卷
- 模拟试卷
- 预测试卷
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.命题“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数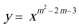
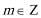
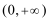
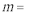
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.给出如下的四个命题:
①

②当

③存在区间


④函数

其中所有正确命题的序号是( )(注:把你认为所有真命题的序号都填上)
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列








正确答案
2009
解析
解析已在路上飞奔,马上就到!
知识点
5.在△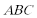
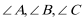
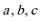
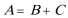
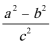
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
10.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数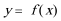
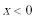
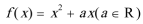
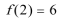
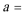
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数
(1)指出图中曲线
(2)若



(3)结合函数图像,判断
15.已知函数

(1) 指出图中曲线
(2) 若



(3) 结合函数图象,判断
的大小关系,并按从小到大的顺序排列。
正确答案
18.某化工厂打算投入一条新的生产线,但需要经过环保部门审批同意后方可投入生产。 已知该厂连续生产


(1)请你代表环保部门给该厂拟定最长的生产周期;
(2)若该厂在环保部门的规定下生产,但需要每月缴纳




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若函数

(2)若




(3)证明:当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.用数学归纳法证明: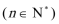
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.数列


(1)当

(2)当


(3)当







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24. 已知函数
(1)求函数

(2)若对任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 设


(1)求
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数
(1)求函数
(2)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数



(1)设


(2)当

正确答案
解析
解析已在路上飞奔,马上就到!