- 真题试卷
- 模拟试卷
- 预测试卷
2.设全集U为实数集R,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知
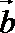
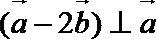
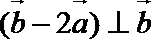
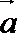
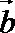
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知命题p:



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.学校准备从5位报名同学中挑选3人,分别担任校运会中跳高、跳远和铅球3个不同项目比赛的志愿者.已知其中同学甲不能担任跳高比赛的志愿者,则不同的安排方法共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在△










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.





正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
15.如图放置的边长为1的正方形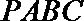



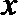
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.执行如图所示的程序框图,输出的
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
13.观察下列各等式:


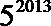
正确答案
3125
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(I)求函数
(II)若


正确答案
解:(Ⅰ )因为 
所以函数


(Ⅱ )因为 
所以 

因为

又因为

所以原式
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=1200.
(1)求证:平面ADE⊥平面ABE ;
(2)求二面角A—EB—D的大小的余弦值.
正确答案
(1)证明:取BE的中点O,AE的中点F
连OC,OF,DF,则2OF
∵ AB⊥平面BCE,CD⊥平面BCE,∴ 2CD 
∴ OF
∵ BC=CE,∴ OC⊥BE,又AB⊥平面BCE,从而
∴ OC⊥平面ABE, ∴ FD⊥平面ABE.
从而平面ADE⊥平面ABE.
(2)取BE的中点O,连OC.∵BC=CE, ∴ OC⊥BE
又AB⊥平面BCE,∴ OF⊥平面BCE.
故可以O为原点建立如图空间直角坐标系O-xyz,
由已知条件有:,

设平面BDE的法向量为
则由
及


∵ 平面ABE的法向量可取为
∴ 二面角A—EB—D的余弦值为

∴ 二面角A—EB—D的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
19.等差数列




(1)求

(2)求
正确答案
:解:(1)设

则

依题意有
解得

故
(2)
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(I)求

(II)若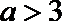

(III)若

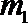


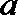
正确答案
:解:(Ⅰ)


(Ⅱ)函数
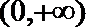
由(Ⅰ)可得
令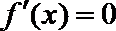

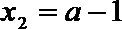
当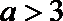
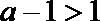
所以单调递增区间为


(Ⅲ)当



所以
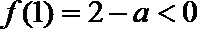
因为函数
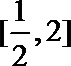
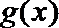

所以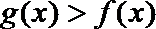

要使存在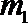


只需要

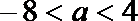
又因为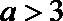


解析
解析已在路上飞奔,马上就到!
知识点
17.某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择是相互独立的.
(I)求甲、乙两人都选择A社区医院的概率;
(II)求甲、乙两人不选择同一家社区医院的概率;
(III)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
正确答案
解:(Ⅰ )设“甲、乙两人都选择A社区医院”为事件

所以甲、乙两人都选择A社区医院的概率为
(Ⅱ )设“甲、乙两人选择同一个社区医院”为事件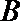
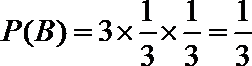
所以甲、乙两人不选择同一个社区医院的概率是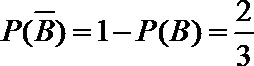
(Ⅲ )依题意
所以ξ的分布列为
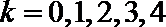
所以 
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆








(Ⅰ)求椭圆
(Ⅱ)设椭圆







正确答案
:解:(I)当

解得:

(II)当



又

据此可得



由此猜测当



证明如下:设点







由方程组

所以:
从而:

所以:以


解析
解析已在路上飞奔,马上就到!



































































