- 真题试卷
- 模拟试卷
- 预测试卷
2. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在解


(1)若

(2)若

(3)若

(4)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 一直线垂直于直线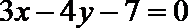
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 下列式子不正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知A是三角形一内角,且
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 下列四个函数中,同时具有性质:① 最小正周期为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知直线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 有以下四个命题:
① 
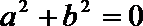
② 若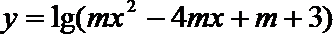
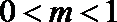
③ 若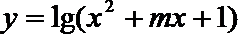
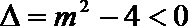
④ 若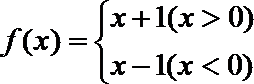
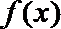
则以上正确命题个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 过点A(0,1)作一直线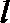
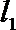


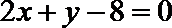

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设坐标原点为O,抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若正数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 






正确答案
∵ 
∴
∴ 

解析
解析已在路上飞奔,马上就到!
知识点
19. 为加快教学手段的现代化,某校计划购置一批电脑,已知甲公司的报价为每台5800元,优惠条件是购买10台以上则从第11台开始可按报价的70%计算;乙公司的报价也是每台5800元,优惠条件是为支持教育每台均按报价的85%计算。假如你是学校的有关负责人,在电脑品牌、质量、售后服务等完全相同的前提下,你将选择购买哪个公司的电脑?
正确答案
设学校计划买电脑
乙公司需付购买费为

① 当
② 当
③ 
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知直线



(1)求

(2)求原点到直线

正确答案
(1)设方程为

∴
当且仅当
(2)
原点到

即:
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知非零向量






(1)当

(2)设数列





正确答案
(1)


(2)∵ 
∴ 
∴ 

∴ 
∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列





(1)求通项公式
(2)若对于任意



正确答案
(1)
即
当
即
(2)
即
化简得


对一切




由


即


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知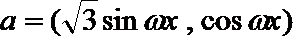
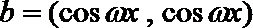
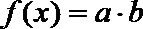
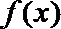
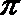
(1)求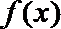
(2)将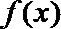
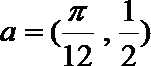
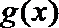
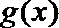
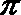
正确答案
(1)
∵ 周期为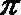
∴ 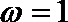
∴ 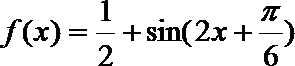
故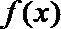

(2)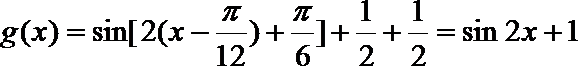
解析
解析已在路上飞奔,马上就到!