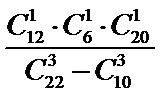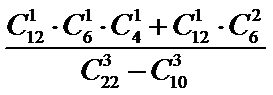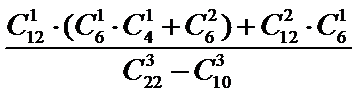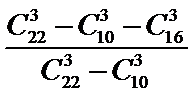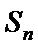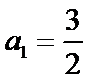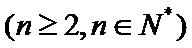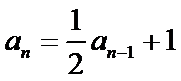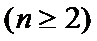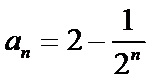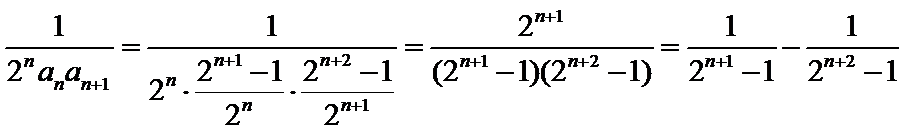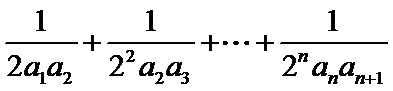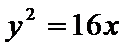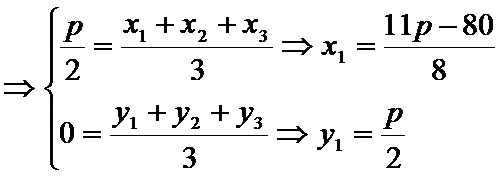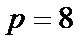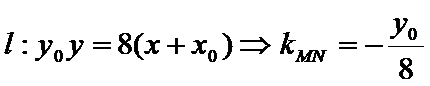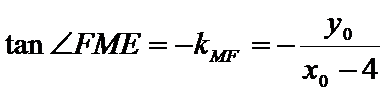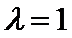- 真题试卷
- 模拟试卷
- 预测试卷
1.复数
正确答案
解析
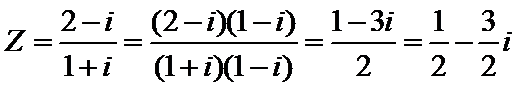
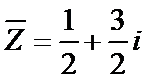
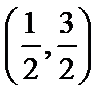
考查方向
解题思路
先利用复数的除法将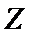
易错点
没有注意到共轭复数这个条件导致选错。
知识点
2. 某程序的框图如图所示,执行该程序,若输入的N =3,则输出i =( )
正确答案
解析










考查方向
解题思路
根据给出的程序框图循环执行,直到不符合条件跳出循环。
易错点
无法确定程序结束的条件导致出错。
知识点
5. 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( )
正确答案
解析
根据三视图将几何体放到正方体中,发现原几何体是由图中菱形的平面截得下边的部分。
由图知,该几何体的体积是正方体体积的一半,所以其体积为
考查方向
解题思路
1、将几何体放到长方体中考虑;
2、得到原来的几何体后求出其体积即可。
易错点
1.无法根据三视图还原成直观图;
2.不会计算得到几何体的体积。
知识点
8.已知实数


正确答案
解析
作出线性约束条件
为图中直线




考查方向
解题思路
1.先作出可行域;
2.在可行域中找到
易错点
1.可行域画错;
2.不能将
知识点
10.某高中数学老师从一张测试卷的12道选择题、4道填空题、6道解答题中任取3道题作分析,则在取到选择题时解答题也取到的概率为( )
正确答案
解析
从12道选择题、4道填空题、6道解答题中任取3道题取到选择题才取法有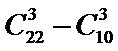
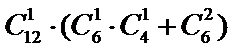
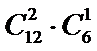
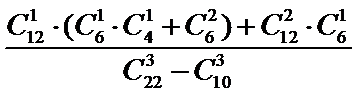
考查方向
解题思路
1.先求任选3道题,取到选择题的解法有多少种;
2.然后求任选的3道题中既有选择题又有解答题的选法有多少种,最后带到古典概型的概率公式中即可。
易错点
1.分类不全,分类没有明确的标准,分类重复等;
2.对于各类情况的算法出错。
知识点
3.设集合

正确答案
解析
集合






考查方向
解题思路
1.先解出集合A,然后解出集合B,进而求出B的补集;
2.利用数轴求出
易错点
1. 解不等式
2. 
知识点
4.函数
正确答案
解析





考查方向
解题思路
1.先将
2.利用对称中心的坐标公式求出对称中心。
易错点
1.误认为对称中心的纵坐标为0,导致误选B;
2.不将
知识点
6.在如图所示的正方形中随机投掷10 000 个点,则落入阴
正确答案
解析
由正态分布N(-1,1)可知,





考查方向
解题思路
1.先利用正态分布求出阴影部分的面积;
2.利用几何概型的概率公式估计落入阴
易错点
1.不理解正态分布的知识导致无法入手;
2.对于几何概型的面积不理解导致出错。
知识点
7.已知数列



正确答案
解析
由




考查方向
解题思路
1.先利用等差数列、等比数列的性质求出


2.将结果带入
易错点
1.将等差数列和等比数列的性质弄混导致出现混乱;
2.三角函数的化简出错。
知识点
9.在△ABC中,内角A,B,C 所对的边分别为 a,b,c,若 cos 2B+cosB=1-cos AcosC 则( )
正确答案
解析
由cos 2B+cosB=1-cos AcosC
得到sin 2B=cos Acos C-cos(A+C)
所以sin 2B=cos Acos C-cos AcosC+sinAsinC
所以sin 2B=sinAsinC
由正弦定理得,b2 = ac,所以a,b,c 成等比数列,故选B。
考查方向
解题思路
1.先利用三角函数中的公式将cos 2B+cosB=1-cos AcosC化简;
2.利用正弦定理得到边之间的关系即可。
易错点
1.对于题中cos 2B+cosB=1-cos AcosC的化简不会入手;
2.对于三角函数的化简出错
知识点
12.已知




正确答案
解析
令
























考查方向
解题思路
1.先求出
2.根据 




易错点
1.无法做出
2. 满足

知识点
11.双曲线
正确答案
解析
由题意得直线








考查方向
解题思路
1.先将直线
2.根据直线与圆相切得到
易错点
不会转化题中的条件:以A1A2为直径的圆内切于菱形F1B1F2B22.在由
知识点
15.已知P,A,B,C是球O球面上的四点,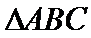
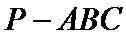
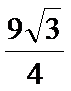
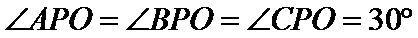
正确答案
解析
由
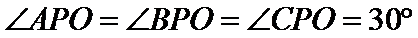
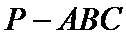
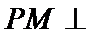
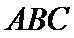
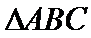
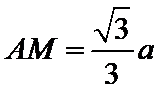
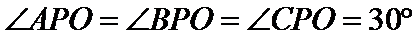
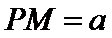
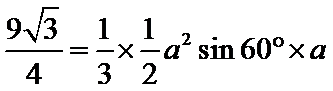
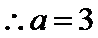

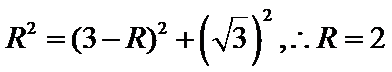
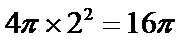
考查方向
解题思路
1.先根据条件判断出三棱锥为正三棱锥,根据体积求出底面边长和高;
2.将球心和半径所在的平面提出来, 利用平面几何的知识求解。
易错点
1.无法根据条件判断出三棱锥为正三棱锥;
2.不能确定球心O所在位置
知识点
14.正





正确答案
解析
设正






考查方向
解题思路
1.先利用


2.构建平面直角坐标系,将所需向量用坐标的形式表示出来,然后求解。
易错点
1. 


2.不能构建平面直角坐标系解决问题。
知识点
16.下列说法中所有正确的序号是________
①、
②、若
③、
④、数列
正确答案
①③④
解析
对于①,

对于②,



对于③,由题意知




对于④,








考查方向
解题思路
逐个判断真假即可。
易错点
1. ②中很容易选错,③感觉无从下手;
2.对于④的单调性不能很好的利用对勾函数的单调性导致无法判断。
知识点
13.设

正确答案
3
解析




考查方向
解题思路
1.求定积分
2.令x=1得到展开式中各项系数和。
易错点
1. 
2.不会求二项式展开式中各项系数和
知识点
17. 已知数列
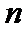
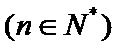
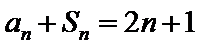
(1)求数列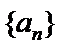
(2)求证: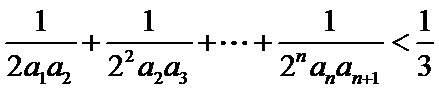
正确答案
(1)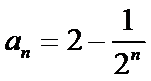
(2)略
解析
(1)∵

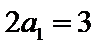
∵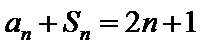
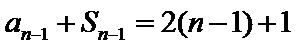
两式相减,得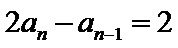
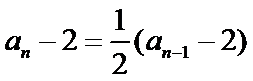
∴数列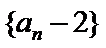
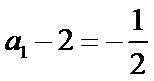
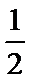
∴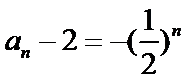
(2)∵
∴
考查方向
本题主要考查与之间的关系,求数列的通项公式、列项相消法求和等知识,意在考查考生的运算求解能力、逻辑推理能力、及综合运用知识解决问题的能力。
解题思路
1.第(1)问先从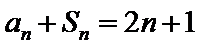
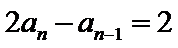
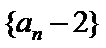
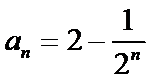
2.第(2)问先将通项公式裂成两项差的形式,然后利用列项相消法求和后即可得到答案。
易错点
1.不会将题中的条件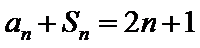
2.不会构造等比数列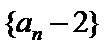
3.第(2)问不会将通项公式裂成两项差的形式,导致无法求和。
知识点
18. 已知正方形









(1)在正方形


(2)从










正确答案
(1)
(2)
解析
(1)这是一个几何概型,点








(2)从


















所以




且



所以随机变量
随机变量
考查方向
解题思路
1.先利用几何概型的概率公式求出满足
2.先求随机变量的取值,然后求其取各个值的概率,列出分布列,带入期望公式求出期望。
易错点
1.第(1)问的概率求错;
2.第(2)问中随机变量取值的概率不会求。
知识点
19. 如图,在三棱柱



(Ⅰ)求证:
(Ⅱ)若四边形



正确答案
(1)略
(2)
解析
(I)证:连结AC1,设AC1与A1C相交于点E,连接DE,则E为AC1中点
∵BC1∥平面A1CD,
∴DE∥BC1
∴ D
又∵
(Ⅱ)
又


又
法一:设BC的中点为O,








则

∴
平面
所以直线A1D与平面CBB1C1所成角的正弦值为
法二:取


∵




延长



则


因为


即直线


法三:取


∵




取



连结BN,∵
∴


∵
即直线

考查方向
解题思路
1.先根据过


2.先证明

易错点
1.第(1)问对于题中给定的条件过


2.第(2)问找不到线面垂直的条件导致无法建坐标系。
知识点
20.已知顶点为原点O,焦点在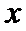
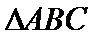
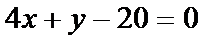
(1)求抛物线方程;
(2)过抛物线上一动点M作抛物线切线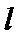
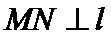
ME(E在M的右侧)平行于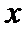
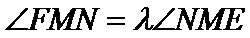
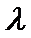
正确答案
(1)
(2)1
解析
(1)设抛物线的方程为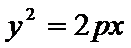
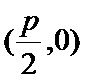
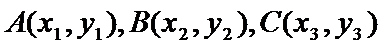
联立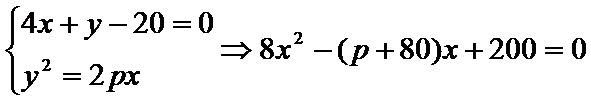
∴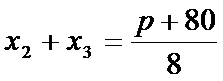

又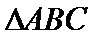
代入抛物线中,
解得
故抛物线方程为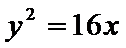
(2)设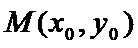
即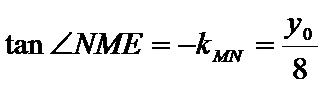
又
∵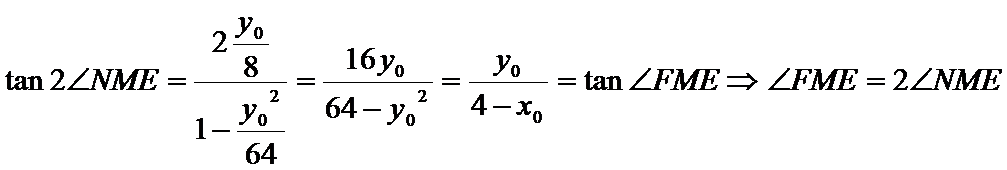
即
考查方向
解题思路
1.第(1)问先设抛物线方程,然后利用待定系数法求出方程;
2.第(2)问先表示出切线l的方程,进而求出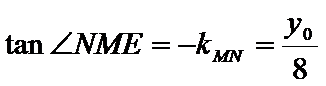
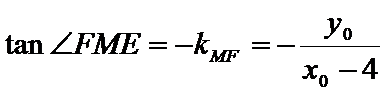
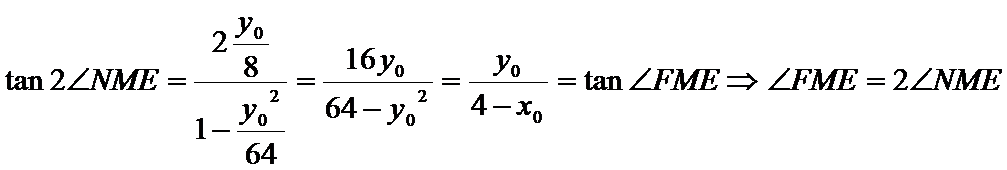
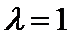
易错点
1.不知道重心坐标和A,B,C坐标间的关系,导致没有思路;
2.不会将角间的关系转化到直线斜率上表示导致无法下手。
知识点
21. 已知函数




(Ⅰ)已知


(Ⅱ)设函数










正确答案
(1)
(2)
解析
解:
(1)






(2)


设













当

当









考查方向
本题主要考查导数在研究函数性质中的应用、导数的几何意义、考查分离参数法,构造函数等知识,意在考查考生综合解决问题的能力。
解题思路
1.第(1)直接利用求导,导数的几何意义直接得到所求的切线方程;
2.第(2)问先设P点坐标后表示出Q点坐标带入

易错点
1.对于
2.不会构造新函数
3.分类讨论的分类标准不会把握。
知识点
22.选修4-1:几何证明选讲
如图所示,AC为⊙O的直径,D为弧BC的中点,E为BC的中点。
(Ⅰ)求证:DE∥AB;
(Ⅱ)求证:AC·BC=2AD·CD
正确答案
(1)略;(2)略
解析
(Ⅰ)连接OE,因为D为弧BC的中点,E为BC的中点,所以OED三点共线。
因为E为BC的中点且O为AC的中点,所以OE∥AB,故DE∥AB。
(Ⅱ)因为D为弧BC的中点,所以∠BAD=∠DAC,
又∠BAD=∠DCB ∠DAC=∠DCB.
又因为AD⊥DC,DE⊥CE △DAC∽△ECD


2AD·CD=AC·2CE
2AD·CD=AC·BC
考查方向
解题思路
1.第(1)问根据三角形的中位线证明出答案;
2.第(2)问先利用同弧、等弧所对的圆周角相等,直径所对的圆周角是直角等证明△DAC∽△ECD,然后利用相似三角形的对应成比例,得到答案。
易错点
1.第(1)问没有发现D,E,O三点共线,导致无法证明;
2.不能发现BC,CE的关系。