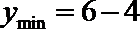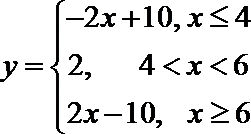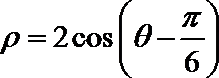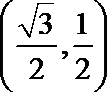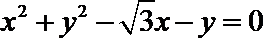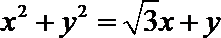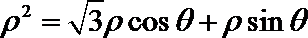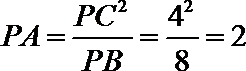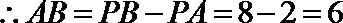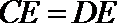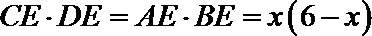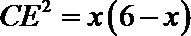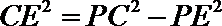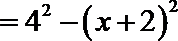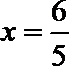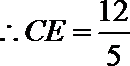- 真题试卷
- 模拟试卷
- 预测试卷
8.在






















正确答案
解析
如下图所示,由于点

设




因此
由于
当且仅当


此时点




因此

故选D.
知识点
2.已知



正确答案
解析
解不等式

解得
故“

故选B.
知识点
4.若函数

正确答案
解析
函数








知识点
6.将函数


正确答案
解析

知识点
1.已知命题


正确答案
解析
由全称命题的否定知,命题



知识点
3.设全集


正确答案
解析
由图象知,图中阴影部分所表示的集合为
由于
故图中阴影部分表示的集合为
故选B.
知识点
5.若



正确答案
解析
作出不等式组
则


联立

由图象知,当直线




即
知识点
7.已知定义在






正确答案
解析
考虑函数

当


由于函数


由于函数




故函数

因此函数

故选D.
知识点
10.函数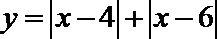
正确答案
解析
解法一:由绝对值的几何意义知,函数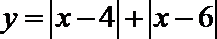
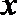
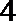
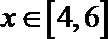
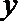
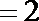
解法二:去绝对值符号得
当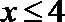
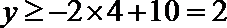
当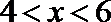
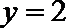
当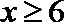
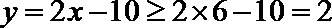
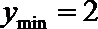
知识点
9.在




正确答案
解析
设
即
由于


知识点
11.设数列




正确答案
解析
由于数列

则数列
且


故
知识点
13.定义:如果函数












正确答案
解析
由题意知,存在
即
故实数

知识点
12.若函数



正确答案
解析
由于函数


由反函数的定义知,函数

知识点
选做题: 第14、15题为选做题, 两题全答的, 只计前一题的得分。
14.以极坐标系中的点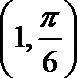
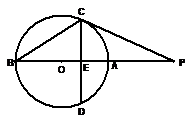
15.如图,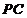
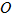
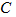
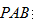
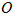
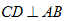
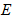
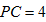
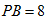
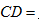
正确答案
14. 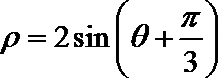
15.
解析
14.
极坐标系中的点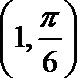
故在以极坐标系中的点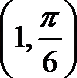
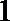
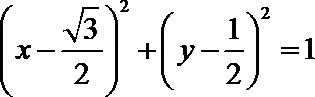
即
化为极坐标方程得
化简得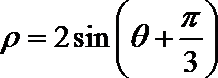
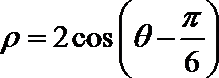
15.
由于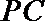
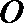
由切割线定理得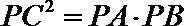
由于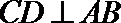
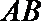
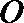
由垂径定理知
设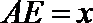
即
由勾股定理得
故有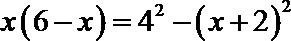
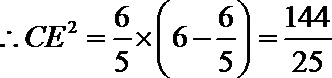
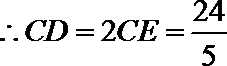
知识点
16.已知



(I)求函数
(II)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在





(I)求函数
(II)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在一般情况下,大桥上的车流速度








(I)当

(II)当车流密度

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设








(1)求通项

(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数








(I)求常数


(II)求证:对于函数



(III)若存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(I)求函数
(II)若函数




正确答案
解析
解析已在路上飞奔,马上就到!