- 真题试卷
- 模拟试卷
- 预测试卷
1.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.给出以下结论:
(1)命题“存在

(2)复数
(3)


(4)已知2013届某市七校联考的数学考试成绩


其中结论正确的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若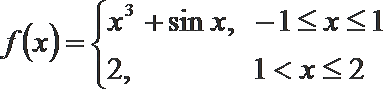

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中,若每盒放2个,则标号为1,6的小球不在同一盒中的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在平面直角坐标系中,已知椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.请在下列两题中任选一题作答.若两题都做,则按第一题评阅计分.
(1)(坐标系与参数方程选做题)
曲线C的极坐标方程为 

(2)(不等式选做题)
已知函数

正确答案
(1)2
(2)
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求常数
(2)在











正确答案
解:(1)
∵ 

∵ 函数


∴当




此时,

(2)∵ 


解得

∵ 


∵ 



由①和②解得
∵
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
17.自“钓鱼岛事件”,中日关系日趋紧张,不断升级.为了积极响应“保钓行动”,学校举办了一场保钓知识大赛,共分两组.其中甲组得满分的有1个女生和3个男生,乙组得满分的有2个女生和4个男生.现从得满分的同学中,每组各任选2个同学,作为保钓行动代言人.
(1)求选出的4个同学中恰有1个女生的概率;
(2)设

正确答案
解:(1)设“从甲组内选出的2个同学均为男同学;
从乙组内选出的2个同学中,1个

“从乙组内选出的2个同学均为男
从甲组内选出的2个同学中1个是男同学,1个为女同

由于事件


∴选出的4个同学中恰有1个女生的概率
(2)

∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
19.已知圆柱







(1)求曲线
(2)当

(3)是否存在



正确答案
解法一:(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线




(2)当


故点

连结AP、BP,OP. 由


从而平面


所以,

在


于是:
所以,点

(3)由于二面角


过

由于




于是



若


令




所以



故不存在




解法二:如图,以O为原点,OB所在直线为x轴,过O与OB垂直的直线为y轴,建立空间直角坐标系。
则


所以



(1)同解法一;
(2)当



又


(3)设

取

由

以下同解法一。
解析
解析已在路上飞奔,马上就到!
知识点
18.已知







(1)求数列

(2)记




正确答案
解:(1)由
且


在

当





(2)






解析
解析已在路上飞奔,马上就到!
知识点
20.设双曲线



(1)求双曲线
(2)若直线





正确答案
解:(1)依题双曲线



又双曲线







(2)设




题意得
(*)设


又










代人(*)式得:
解得:



故所求

解析
解析已在路上飞奔,马上就到!
知识点
21.设函数
(1)若函数


(2)若函数


(3)求证:当


正确答案
解: 





(1)依题: 
(2)依题: 
(3)由(2)知:当






取


即有:
解析
解析已在路上飞奔,马上就到!






































































