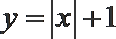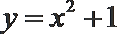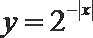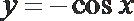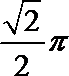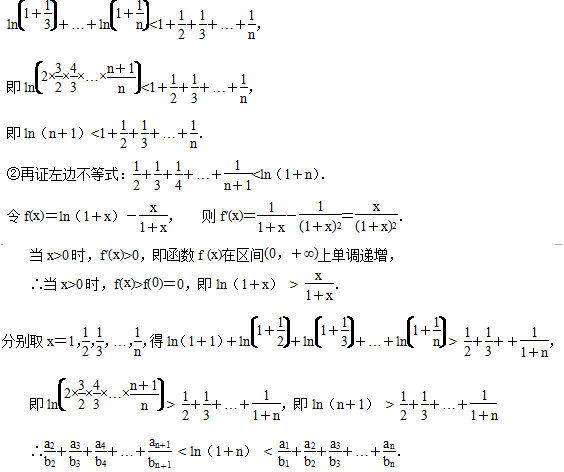- 真题试卷
- 模拟试卷
- 预测试卷
1.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列函数中,既是偶函数、又在区间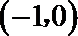
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.离散型随机变量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一空间几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.有四个关于三角函数的命题


其中假命题的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知向量
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
11.


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
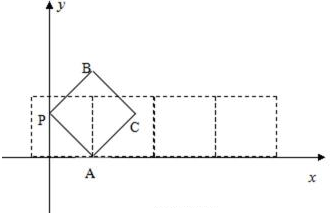
13.如图放置的边长为1的正方形PABC沿x轴滚动。设顶点P(x,y)的轨迹方程是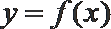
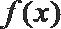
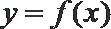
正确答案
4;
解析
解析已在路上飞奔,马上就到!
知识点
选做题:第14、15题为选做题,只能选做其中的一题,两题全答的,只计算前一题的得分.
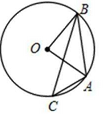
14.(几何证明选讲选做题)
如图,点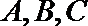
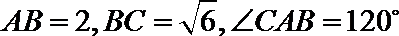
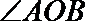
15.(坐标系与参数方程选做题)
在极坐标系中,圆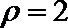
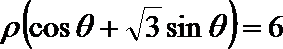
正确答案
14.
15. 1
解析
解析已在路上飞奔,马上就到!
知识点
12.如图所示,程序框图(算法流程图)的输出结果是________.
正确答案
14
解析
解析已在路上飞奔,马上就到!
知识点
17.在



(I)求角
(II)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在三棱锥






(Ⅰ)证明:
(Ⅱ)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列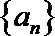
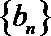
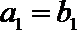
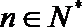
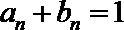
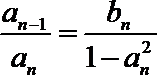
(1)求数列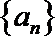
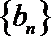
(2)证明: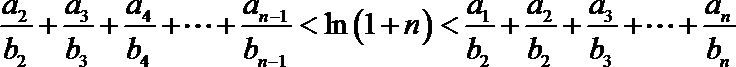
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数


(Ⅰ)求
(Ⅱ)若方程



(Ⅲ)令










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知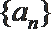
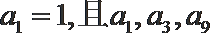
(Ⅰ)求数列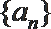
(Ⅱ)求数列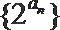
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为




(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求

(Ⅲ)求数学期望
正确答案
解析
解析已在路上飞奔,马上就到!