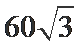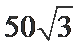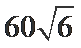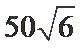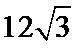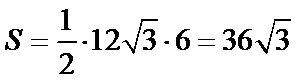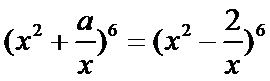- 真题试卷
- 模拟试卷
- 预测试卷
2.已知

正确答案
解析



考查方向
解题思路
先将复数的一般形式表示出来,然后确定其在复平面的位置
易错点
忽略
知识点
5.一个多面体的三视图分别是正方形、等腰三角形和矩形,其尺寸如图,则该多面体的体积为( )
正确答案
解析
由三视图可知,该几何体是一个横放的直三棱柱,所以
代入数值可得,体积为48,所以选A
考查方向
解题思路
先根据三视图还原成空间几何体,再根据所给长度计算体积
易错点
立体感不强,计算错误
知识点
6. 已知




正确答案
解析
根据函数的图象的相邻两条对称轴之间的距离等于






考查方向
解题思路
先求出周期w,再由条件求出
易错点
三角函数周期,同角三角函数转换错误。
知识点
7. 阅读如图所示的程序框图,若输入

正确答案
解析
第1次,
第2次,
…………
第n次,
所以当输入 
考查方向
解题思路
根据程序框图的流程,计算运行n次的结果,根据输入的数值,判断n满足的条件,从而求出输出的值
易错点
选择语句判断错误
知识点
9.若x,y满足
正确答案
解析
所求区域如下图,可知B(2,0)点为最大值点,所以kx-y+3=0,代入直线可得2k+3=0,所以k=
考查方向
解题思路
根据已知的约束条件,画出满足约束条件的可行域,再用目标函数的几何意义求解K的值
易错点
可行域区域作图错误,找不到最佳点
知识点
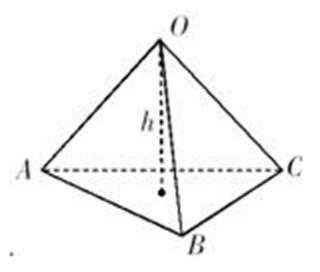
10.球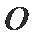
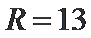

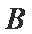
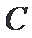
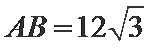
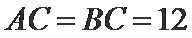
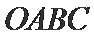
正确答案
解析
球心O与A,B,C,三点构成的四面体如下图所示,所以底面ABC的面积为底乘以高,底为AB=
高为6,因为球的半径为13,所以圆心到面ABC的距离为12,所以底面面积为
所以体积为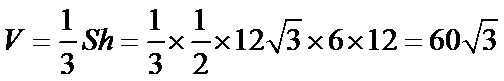
考查方向
解题思路
先根据题意作出四面体大致图形,然后利用体积公式求解
易错点
空间感不强;计算错误
知识点
1.设集合



正确答案
解析
因为

考查方向
解题思路
根据题意,先确定集合M和N表示的x的范围,然后在求交集和补集
易错点
集合的基本概念理解不透彻
知识点
3
①“p∨q”为真是“¬p”为假的必要不充分条件;
②“




其中说法正确的是( )
正确答案
解析
对于命题1,由¬p为假可以推出p∨q为真,但由p∨q为真不能推出¬p为假的值,所以前者是后者的必要不充分条件,命题1正确。易得命题2也是正确的。所以选C
考查方向
解题思路
根据相关性质,逐一判断
易错点
对逻辑与命题理解不透彻;
知识点
4.下列函数中,既是偶函数,又在
正确答案
解析
由函数的奇偶性及单调性的性质可知,B和D选项为偶函数,又知,D选项在
考查方向
解题思路
根据函数单调性及奇偶性的性质,逐个选项判断
易错点
函数单调性判断错误,函数奇偶性判断错误
知识点
8.过双曲线








正确答案
解析
由题意可知P(-1,0),所以直线L的方程为y=x+1,两条渐近线的方程为y=-bx或y=bx,所以可得Q点横坐标为

所以

C=

考查方向
解题思路
先求出R和Q的横坐标,然后求出b的值,进而求出c,然后根据离心率公式答案可得
易错点
计算能力弱,离心率公式记混淆
知识点
11.如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
正确答案
解析
如图可知,CD=150,OD=100,
在三角形CDO中,
考查方向
解题思路
由余弦定理求OC的长度
易错点
计算错误;实际问题不能转换成数学模型
知识点
12.已知函数



正确答案
解析




因为





考查方向
解题思路
利用函数的性质将不等式恒成立转换成其他等价形式,由
易错点
求导错误,讨论参数取值范围时考虑不全面
知识点
某市规定,高中学生三年在校期间参加不少于






19.求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
20.从全市高中学生(人数很多)中任意选取3位学生,记



正确答案
见解析
解析
根据题意,参加社区服务时间在时间段





考查方向
解题思路
第1问根据样本数据估计总体数据,第2问先把所有可能的情况列出来,然后用频率求概率
易错点
数据收集整理出错
正确答案
见解析
解析
由19题可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小
时的概率为


所以



随机变量
因为

考查方向
解题思路
第1问根据样本数据估计总体数据,第2问先把所有可能的情况列出来,然后用频率求概率
易错点
数据收集整理出错
已知抛物线











23.分别求抛物线

24.经过








正确答案
见解析
解析
由已知抛物线



设椭圆






考查方向
解题思路
第一问根据离心率及焦点求抛物线C和椭圆E的方程,第二问利用平面向量的数量积的坐标公式证明线段和线段垂直。
易错点
计算错误,利用平面向量证明线段垂直
正确答案
见解析
解析
显然直线


故可设直线


由



∵抛物线


∴过抛物线



即

解得两条切线




∴
考查方向
解题思路
第一问根据离心率及焦点求抛物线C和椭圆E的方程,第二问利用平面向量的数量积的坐标公式证明线段和线段垂直。
易错点
计算错误,利用平面向量证明线段垂直
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
17.求数列{an}的通项公式;
正确答案
见解析
解析
考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等差数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而求出bn的前n项和。
易错点
求数列通项公式错误
正确答案
见解析
解析
考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等差数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而求出bn的前n项和。
易错点
求数列通项公式错误
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC 的中点.
21.求证:AE⊥PD;
22.若直线PB与平面PAD所成角的正弦值为
正确答案
见解析
解析
证明:由四边形



因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA

而PA

所以 AE⊥平面PAD,又PD
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
正确答案
见解析
解析
由21知AE,AD,AP两两垂直,以








所以




由





解得



设平面AEF的一法向量为m=(x1,y1,z1),则







所以

因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
已知函数
25.若函数


26.令





27.当
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
选修4—1,几何证明选讲
圆












28.求证:△

29.如果

正确答案
见解析
解析
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析





考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
13.已知圆x2+y
正确答案
-4
解析
圆的标准方程为:

考查方向
解题思路
把圆的方程转化为标准形式,求出弦心距,再由条件根据弦长公式求得a的值
易错点
计算错误
知识点
14.将序号为1,2,3,4的四张电影票全部分给3人,每人至少一张.要求分给同一人的两张电影票连号,那么不同的分法种数为 .(用数字作答)
正确答案
18
解析
由题意可知,3人分4张票,且每人至少1张,至多两张,则2人一张,一人2张,且分的的票必须是连号,相当于将1、2、3、4这四个数用2个板子隔开,在三个空位插2个板,所以共有3种情况,再对应到3个人,有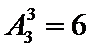
考查方向
解题思路
利用分步计算原理,由排列知识确定不同的分法数。
易错点
考虑情况不全
知识点
15.设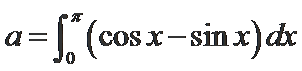
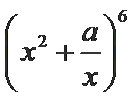
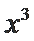
正确答案
-160
解析
因为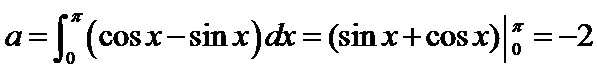
因为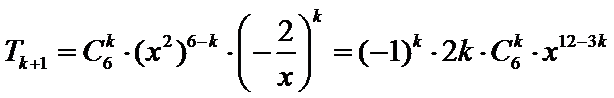
所以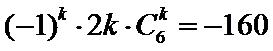
考查方向
解题思路
根据微积分基本定理首先求出a的值,然后根据二项式的通项公式求出系数的值
易错点
计算错误,积分积不出来
知识点
16.已知数列





正确答案
解析
因为,

即有
即
考查方向
解题思路
由数列的通项和前n项和的关系,结合条件化简整理,再根据等差数列的定义和通项,即可得到Sn,进而求出答案
易错点
找不到通项与前n项和的关系,计算错误