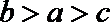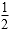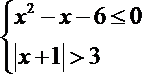- 真题试卷
- 模拟试卷
- 预测试卷
1. 设集合A＝{x|1＜x＜4}，B＝{x|x 2－2x－3≤0}，则A∩(
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3. 函数
A
B[0，2]
C[1，+
D[0，+
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7. 设函数f(x)＝x3＋sin x，若0≤θ≤时，f(mcos θ)＋f(1－m)>0恒成立，则实数m的取值范围是（ ）
A( 0 , 1 )
B(－∞，0)
C(－∞，1)
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5. 设当x∈(1,2)时，不等式(x－1)2<logax恒成立，则a的范围是（ ）
A(0,1)
B(1,2)
C(1,2]
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4. 已知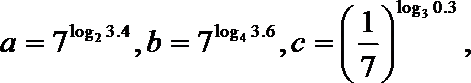
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6． f(x)是定义在R上的奇函数，且满足f(x＋2)＝f(x)，又当x∈(0,1)时，f(x)＝2x－1，则
A－5
B－6
C－
D－
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2. 已知命题p：函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．直线
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
11．已知集合A＝{x||x－1|<2}，B＝{x| 
正确答案
（－1，＋∞）
解析
解析已在路上飞奔，马上就到！
知识点
12. 若存在实数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13. 已知函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10. 已知函数f(x)＝ax4＋bcos x－x，且f(－3)＝7，则f(3)的值为________．
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
14. 若直角坐标平面内两点P，Q满足条件：
①P、Q都在函数f(x)的图象上；
②P、Q关于原点对称，则称点对(P，Q)是函数f(x)的一个“友好点对”(点对(P，Q)与点对(Q，P)看作同一个“友好点对”)．
已知函数f(x)＝
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
15. 给出定义：若
①函数y＝f(x)的定义域为R，值域为
②函数y＝f(x)的图象关于直线
③函数y＝f(x)是周期函数，最小正周期为1；
④函数y＝f(x)在
其中正确的命题的序号是________．
正确答案
①②③
解析
解析已在路上飞奔，马上就到！
知识点
17.在
（Ⅰ）求tanC的值；
（Ⅱ）若a＝
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况。在一般情况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数。当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时。研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数。
（1）当0≤x≤200时，求函数v(x)的表达式；
（2）当车流密度x为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/小时)f(x)＝x·v(x)可以达到最大，并求出最大值。(精确到1辆/小时)
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16.设命题p：实数x满足x2－4ax＋3a2<0，其中a>0，命题q：实数x满足
（1）若a＝1，且p且q为真，求实数x的取值范围；
（2）非p是非q的充分不必要条件，求实数a的取值范围．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18.已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分．现从该箱中任取3个球(无放回，且每球取到的机会均等)，记随机变量X为取出3球所得分数之和．
（Ⅰ）求X的分布列；
（Ⅱ）求X的数学期望E(X)．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
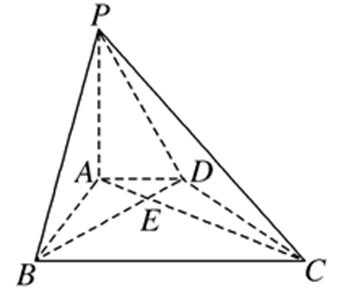
19.如图，在底面为直角梯形的四棱锥P－ABCD中，AD∥BC，∠ABC＝90°，PA⊥平面ABCD，PA＝3，AD＝2，AB＝2，BC＝6.
（1）求证：BD⊥平面PAC；
（2）求平面PBD与平面BDA所成的二面角大小．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21.已知函数f(x)＝－x2＋8x，g(x)＝
（1）求f(x)在区间[t，t＋1]上的最大值h(t)；
（2）是否存在实数k,对任意的
正确答案
解析
解析已在路上飞奔，马上就到！