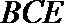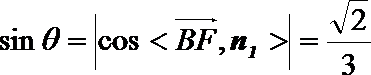- 真题试卷
- 模拟试卷
- 预测试卷
7.点P在边长为1的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知某几何体的三视图如图所示,则其体积为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若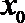
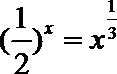
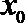
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.定义在R上的函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知i是虚数单位,满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在△ ABC中,M为AC中点,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在△ ABC中,a,b,c是三个内角,A,B,C所对的边,若

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.若命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.对某校400名学生的体重(单位:kg)进行统计,得到如图所示的频率分布直方图,则学生体重在60kg以上的人数为( )
正确答案
100
解析
解析已在路上飞奔,马上就到!
知识点
12.若实数x、y满足
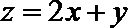
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
15.给定区间D,对于函数









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)求函数
(Ⅱ)求


(Ⅲ)设






正确答案
(Ⅰ)由


则


单调递减区间为
(Ⅱ)令
则

记
因为当



又因为
所以当



所以


所以
(Ⅲ)因为




所以函数


且对


因为

所以
在(Ⅱ)的结论中,取

则有
由

构造函数
则由①得
因为
所以
所以
因为
综上得
解析
解析已在路上飞奔,马上就到!
知识点
21.本题有(1)、(2)、(3)三个选答题,请考生任选2题作答。如果多做,则按所做的前两题记分。
(1)选修4—2:矩阵与变换
已知二阶矩阵


(Ⅰ)求距阵M;
(Ⅱ)设曲线C在矩阵M的作用下得到的方程为
(2)选修4—4:坐标系与参数方程
在直角坐标系


(Ⅰ)求曲线C的普通方程和曲线P的直角坐标方程;
(Ⅱ)设曲线C和曲线P的交点为A、B,求|AB|。
(3)选修4—5:不等式选讲
已知函数


(Ⅰ)求实数t的取值范围;
(Ⅱ)记t的最大值为T,若正实数a、b、c满足

正确答案
(1)选修4-2:矩阵与变换
(Ⅰ)依题意得:

解得

(Ⅱ)设曲线




则

又因为

整理得曲线

(2)选修4-4:坐标系与参数方程
(Ⅰ)曲线



(Ⅱ)曲线



则圆心到直线

(3)选修4-5:不等式选讲
(Ⅰ)不等式


又因为


所以

(Ⅱ)由(Ⅰ)知,

由柯西不等式知:

所以

当且仅当


解析
解析已在路上飞奔,马上就到!
知识点
17.设椭圆

(Ⅰ)求椭圆 C的离心率;
(Ⅱ)若过A、B、F2三点的圆恰好与直线

正确答案
(Ⅰ)由题意知


因为


又因为


又


(Ⅱ)由(Ⅰ)知





所以



所以椭圆的标准方程为:
由


解析
解析已在路上飞奔,马上就到!
知识点
18.已知全集
(Ⅰ)求集合U的非空子集的个数;
(Ⅱ)若集合M={2,3},集合N满足



正确答案
(Ⅰ)集合

(Ⅱ)

满足条件的集合

则每个随机变量









所以

解析
解析已在路上飞奔,马上就到!
知识点
16.在△ ABC的三个内角A、B、C所对的边分别a、b、c,
(Ⅰ)求角C的大小;
(Ⅱ)当

正确答案
(Ⅰ)因为

因为


又因为


(Ⅱ)由(Ⅰ)知,
所以
=

因为

所以

解析
解析已在路上飞奔,马上就到!
知识点
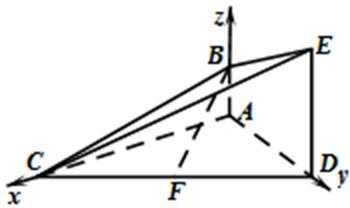
19.已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等腰直角三角形,AC⊥AD,且AD=DE=2AB,F为CD中点。
(Ⅰ)求证:平面BCE⊥平面CDE;
(Ⅱ)求直线BF和平面BCE所成角的正弦值。
正确答案
以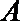
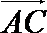
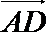
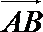
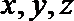
设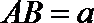
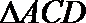
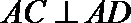
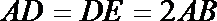
所以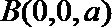
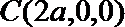
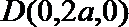
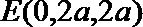
所以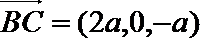
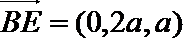
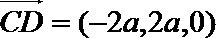
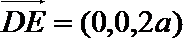
(Ⅰ)设平面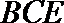
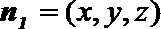
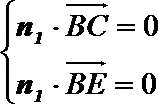
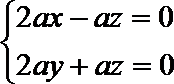
令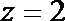
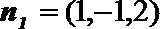
设平面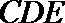
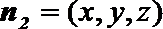
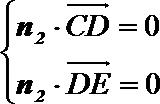
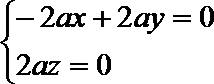
令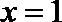
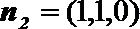
所以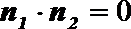
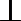
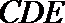
(Ⅱ)因为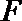
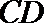
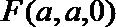
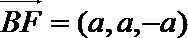
则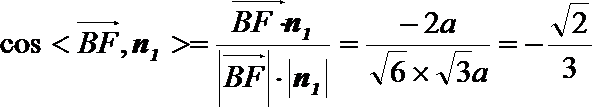
设直线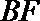
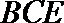
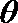
所以直线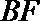
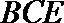
解析
解析已在路上飞奔,马上就到!