- 真题试卷
- 模拟试卷
- 预测试卷
7.设x,y满足约束条件


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
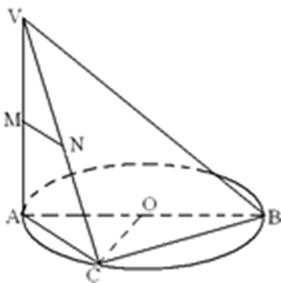
10.如图,AB是⊙O的直径,VA垂直⊙O所在的平面,C是圆周上不同于A、B的任意一点,M、N分别为VA、VC的中点,则下列结论正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知两点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知两定点A(-2,0)和B(2,0),动点P(x,y)在直线L:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知双曲线



则下列各式成立的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设全集U=R,集合A={x|y=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若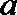
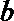
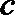
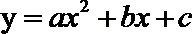
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一个四棱锥的三视图如图所示,其中正视图是腰长为1的等腰直角三角形,则这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.设函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
64
解析
解析已在路上飞奔,马上就到!
知识点
16.已知定义在R上的函数








正确答案
-5
解析
解析已在路上飞奔,马上就到!
知识点
19.四棱锥








(1)求证:

(2)求平面

正确答案
解:
(1)连接






在







(2)以




设平面
由
令

同理设平面

由


设平面


解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求函数
(2)设函数


正确答案
解:
(1)







(2)假设存在

①当




②当




③当













综上所述,存在
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在

(1)求sin
(2)求AC边的长。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.直线

(1)求实数
(2)是否存在实数


正确答案
解:
(1)将直线



整理得
依题意,直线

故
(2)设
则由①式得
假设存在实数



整理得
将②式及


可知存在

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分。
22.如图,已知⊙O的直径AB垂直于弦CD于E,连接AD、BD、OC、OD,且OD=5.
(1)若
(2)若

23.以直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,已知直线L的极坐标方程为


(1)求直线L的直角坐标方程和曲线C的普通方程;
(2)若直线L与曲线C交于A、B两点,求线段AB的长。
24.已知函数
(1)求不等式
(2)若关于x的不等式

正确答案
22.
解:(1)因为
所以

又

因为
所以

(2)因为


所以
因为

设


因为



故
23.
解:(1)因为


因为
(2)联立方程

所以
24.
解:(1)求不等式

得

解得

即不等式的解集为
(2)
即



故实数
解析
解析已在路上飞奔,马上就到!
知识点
18.近年来,政府提倡低碳减排,某班同学利用寒假在两个小区逐户调查人们的生活习惯是否符合低碳观念.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”.数据如下表(计算过程把频率当成概率).

(Ⅰ) 如果甲、乙来自



(Ⅱ)





正确答案
解:
(Ⅰ)设事件



(Ⅱ)设


故低碳族的概率




因随机地从



解析
解析已在路上飞奔,马上就到!