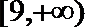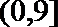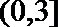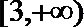- 真题试卷
- 模拟试卷
- 预测试卷
8. 已知y = f (x)是定义在(–2,2)上的偶函数,且f (x)在[0,2)上是增函数,若f (m–2) – f(m + 1)<0,则实
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知直线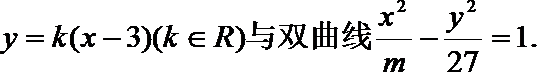
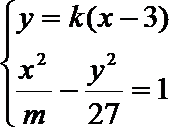
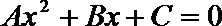
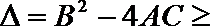
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 关于平面向量的命题
①







②如




③




④





其中正确命题个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设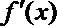

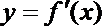
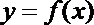
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
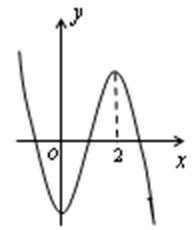
4. 函数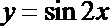

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知F1、F2分别为双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 若数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 如图所示,正方形ABCD中,E、F分别是AB、AD的中点,将此正方形沿EF折成直二面角后,异面直线AF与BE所成角的余弦值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知



(Ⅰ)求函数

(Ⅱ)当

正确答案
(Ⅰ)


(Ⅱ)


若

若


解析
解析已在路上飞奔,马上就到!
知识点









(Ⅰ)求实数

(Ⅱ)求切线长
(Ⅲ)是否存在以



正确答案
(Ⅰ)连接





化简得实数


(Ⅱ)由






(Ⅲ)


















解析
解析已在路上飞奔,马上就到!
知识点










(Ⅰ)求证:平面

(Ⅱ)求直线

(Ⅲ)求点

正确答案
(Ⅰ)设







∴



∴



∴





∵


(Ⅱ)连结









从而



在

在

所以有
即直线

(Ⅲ)由于








从而点


解法二:如图所示,以点








(Ⅰ)由于












(Ⅱ)设


由于


令


再设直线


而

因此直线

(Ⅲ)由(Ⅱ)知


所以点

解析
解析已在路上飞奔,马上就到!
知识点
22. 设函数
(Ⅰ)若x=时,

(Ⅱ)若

(Ⅲ)设






正确答案
答案: 
(Ⅰ)因为









<


所以结论成立.
解析
解析已在路上飞奔,马上就到!
知识点
20.某车间有50名工人,要完成150件产品的生产任务,每件产品由3个







(1)设完成




(2)为了在最短时间内完成全部生产任务,
正确答案
(1)生产150件产品,需加工A型零件450个,
则完成A型零件加工所需时间
生产150件产品,需加工
则完成
(2)设完成全部生产任务所需时间为



令


所以,当



故
当



则


当



则





解析
解析已在路上飞奔,马上就到!
知识点
21. 如图,直角梯形ABCD中,∠


(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)



正确答案
(Ⅰ)以AB中点为原点O,AB所在直线为x轴,建立直角坐标系,如图则A(-1,0),B(1,0), D(-1,

得
所求椭圆F方程
(Ⅱ)由
代入

即



得 


解法2, 设

①—② 得
设




由③、④得 
又
解析
解析已在路上飞奔,马上就到!