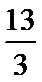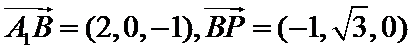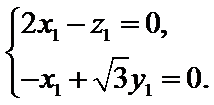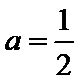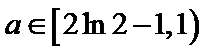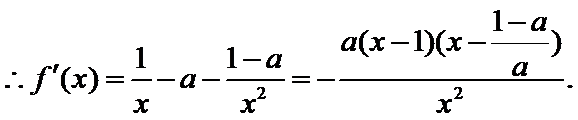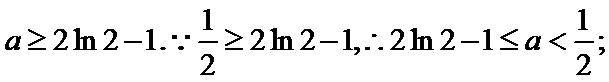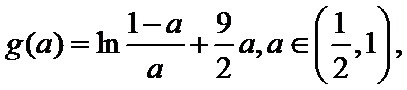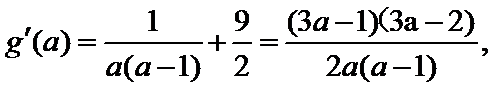- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合A={x|1<x<2},B={x|x<a},若A∩B=A,则a的取值范围是( )
正确答案
解析
由A∩B=A知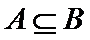
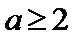
因此,A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
利用A∩B=A得出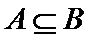
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
对A∩B=A的处理出错
知识点
3.实数a=3是直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行的( )
正确答案
解析
若直线ax+2y+3a=0和直线3x+(a-1)y=a-7平行,则有
考查方向
解题思路
先求出两直线平行时的充要条件(a=3),再判断a=3是该条件成立的什么条件。
因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
易忽视两直线重合的情况
知识点
4.设向量a=(1,m),b=(m-1,2),且a≠b,若(a-b)⊥a,则实数m=( )
正确答案
解析
根据已知得



因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先计算出

因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
两向量坐标运算求出m的值后易忽视对m的值进行验证。
知识点
5.已知焦点在x轴上的椭圆方程为
正确答案
解析
由已知得a>0且4a> 


考查方向
解题思路
先根据焦点在x轴上求出a的取值范围为

易错点
易忽视4a>
知识点
7.执行如图(1)所示的程序框图,则输出的结果为( )
正确答案
解析
当k分别取1,2,3,4,5,6时对应的s的值分别为3,9,21,45,93,189,此时满足s>30k,所以输出的s的值为189.
因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
分别列出k与s的对应值 ,再根据循环条件确定输出时s的值
因此B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
做循环结构的程序框图试题时,一定要注意输出的条件,否则会造成失误。
知识点
9.若函数f(x)=4sinωx·


正确答案
解析
由已知得:



因此A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先化简得


易错点
三角函数在某个给定区间递增或递减,不能正确转化满足条件的不等式。
知识点
1.复数z=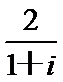
正确答案
解析
由Z=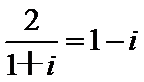
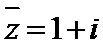
考查方向
解题思路
先计算出复数Z,再写出它的共轭复数。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
写错共轭复数
知识点
6.设a=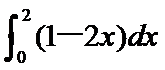
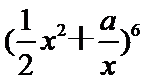
正确答案
解析
由已知得a=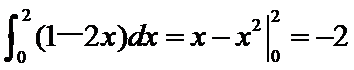
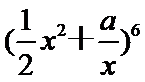
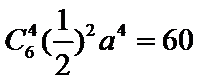
考查方向
解题思路
先根据定积分求出a的值为-2,再利用二项展开式解得常数项为60
因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
二项式定理的展开式易出错
知识点
8.某几何体的三视图如图(2)所示,则该几何体的体积为( )
正确答案
解析
根据三视图还原几何体为一个长方体、三棱锥、四分之一圆柱构成(如图),由图中数据可算出该几何体的体积为:
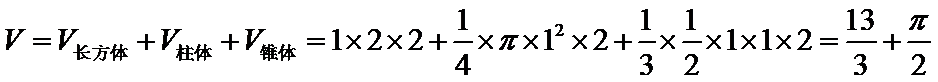
考查方向
解题思路
根据三视图还原几何体为一个长方体、三棱锥、四分之一圆柱构成,由图中数据可算出该几何体的体积。
因此A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
不能通过三视图准确地还原几何体。
知识点
12.若函数f(x)=

正确答案
解析
由f(x)=0知









考查方向
解题思路
把函数f(x)的零点问题转化为两个函数的交点问题,再利用函数的导数探究单调性,从而探索出两个函数的有三个交点时a的取值范围。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
难于构造出两个函数的交点问题。
知识点
10.若函数f(x)=

正确答案
解析
由已知得






因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
先写出分段函数的解析式为:
易错点
对分段函数的单调性分析不准确。
知识点
11.如图(3)所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图像大致是( )
正确答案
解析
在



因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
先根据MN∥平面DCC1D1构造出点E,通过相似比求出ME,从而找到x,y之间的关系式。因此A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
易忽视x的取值范围。
知识点
14.某校高二年级有5个文科班,每班派2名学生参加年级学生会选举,从中选出4名学生 进入学生会,则这4名学生中有且只有两名学生来自同一个班级的概率为___________.
正确答案
解析
高二年级的5个文科班级每班派2名同学参加年级学生会选举,共有10名学生,从中选出4名学生进入学生会共有

考查方向
解题思路
分别计算出从10名学生中选出4名学生进入学生会的基本事件总数和满足这4名学生中有且只有两名学生来自同一班级的基本事件个数,代入古典概率计算公式,可得答案。
易错点
4名学生有且只有两名来自同一个班的基本事件数易算错。
知识点
15.设x,y满足约束条件

____________.
正确答案
解析
令x=u,y=



可行域中的点到原点的距离最小值为原点到直线



考查方向
解题思路
先根据条件

易错点
对于条件
知识点
16.在双曲线
正确答案
解析
由题意,F(c,0),B(0,b),则直线BF的方程为bx+cy-bc=0,若在线段BF上存在点P,使得△PA1A2构成以A1A2为斜边的直角三角形,则

考查方向
解题思路
根据题意写出线段BF所在直线方程,借助△PA1A2构成以A1A2为斜边的直角三角形构建原点到直线的距离小于或等于a,从而解出e的取值范围。
易错点
△PA1A2构成以A1A2为斜边的直角三角形的转化
知识点
13.△ABC的内角A,B,C的对边分别为a,b,c且ac=

正确答案
解析
由ac=






考查方向
解题思路
由ac=




易错点
忽视隐含条件
知识点
已知{

17.求数列{

18.若-

正确答案
(1)
解析
解:(Ⅰ)由题意,
代入得




所以
考查方向
解题思路
(1)通过等差等比数列的定义求出d和q,(2)先求出
易错点
寻找
正确答案
(2)
解析
解:
(Ⅱ)记
所以

所以

所以
考查方向
解题思路
(1)通过等差等比数列的定义求出d和q,(2)先求出
易错点
寻找
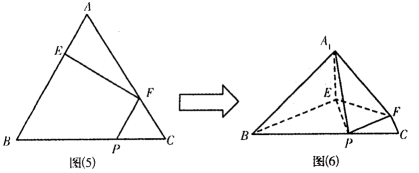
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE :EB=CF :FA=CP :PB=1 :2,如图(5).将△AEF沿EF折起到△A1EF的位置,使二面角A1一EF-B成直二面角,连结A1B、A1P,如图(6).
21.求证:A1E⊥平面BEP;
22.求二面角B—A1P—E的余弦值.
正确答案
(1)A1E⊥平面BEP;
解析
解:不妨设正三角形ABC 的边长为 3 .
(1)在图5中,取BE的中点D,连结DF.
∵AE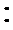
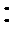
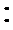
又AE=DE=1,∴EF⊥AD
在图6中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP
考查方向
解题思路
(1)不妨设正三角形ABC 的边长为 3,取BE的中点D,连接DF,从而证明到EF⊥AD,再利用二面角A1一EF-B成直二面角推出A1E⊥BE,从而得证。
(2)由(1)构建空间直角坐标系并写出相关点的坐标,通过计算平面法向量的方法来计算二面角的余弦值。
易错点
平面翻折到空间中的不变量与改变量易出错及空间点坐标的确定。
正确答案
(2) 二面角B-A1P-E余弦值是
解析
解:
(2)建立分别以EB、EF、EA1为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A1(0,0,1),
B(2,0,0),F(0, 
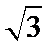
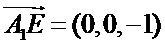

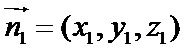
由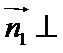
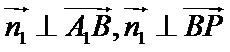
令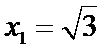

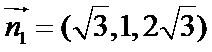
设平面A1PE向量为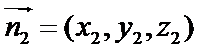
由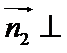
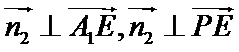


考查方向
解题思路
(1)不妨设正三角形ABC 的边长为 3,取BE的中点D,连接DF,从而证明到EF⊥AD,再利用二面角A1一EF-B成直二面角推出A1E⊥BE,从而得证。
(2)由(1)构建空间直角坐标系并写出相关点的坐标,通过计算平面法向量的方法来计算二面角的余弦值。
易错点
平面翻折到空间中的不变量与改变量易出错及空间点坐标的确定。
如图(7),已知抛物线C:
23.当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5),求p的值;
24.以AB为直径的圆交x轴于M,N两点,记劣弧

正确答案
(1)
解析
解:(1)



设







考查方向
解题思路
(1)首先设出直线AB方程,再计算出中点从而确定其中垂线方程,最后将Q点坐标代入方程算出P的值(2)根据题意设出直线L的方程,表示出弦AB和圆心D的坐标;令


易错点
对条件
正确答案
(2)
解析
解:
(2)设




令


当


故

考查方向
解题思路
(1)首先设出直线AB方程,再计算出中点从而确定其中垂线方程,最后将Q点坐标代入方程算出P的值(2)根据题意设出直线L的方程,表示出弦AB和圆心D的坐标;令


易错点
对条件
某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现采用分层抽样的方法从该年级抽取100名学生进行问卷调查.根据问卷取得了这100名学生每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:①[0,30),② [30,60),③[60,90),④[90, 120),……得到频率分布直方图(部分)如图(4).
19.如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的100名学生,完成下列2×2列联表;并判断是否有95%的把握认为学生利用时间是否充分与走读、住宿有关?
20.若在第①组、第②组、第③组中共抽出3人调查影响有效利用时间的原因,记抽到“有效学习时间少于60分钟”的学生人数为X,求X的分布列和数学期望.
正确答案
(1)
由于K2>3.841,所以有95%的把握认为学生利用时间是否充分与走读、住宿有关
解析
解:(1)
K2=
由于K2>3.841,所以有95%的把握认为学生利用时间是否充分与走读、住宿有关
考查方向
解题思路
(1)根据走读生和住宿生的样本数完成表格,并由表格计算K2确定相关程度
(2)首先计算出第①组、第②组、第③组各抽取的人数,再确定随机变量X的所有可能取值并计算其概率完成分布列,最后计算数学期望。
易错点
各组人数的确定和离散型随机变量的概率的计算
正确答案
(2)
解析
(2)设第i组的频率为Pi(i=1,2,…,8),则由图可知:P1=





则X的所有可能取值为0,1,2,3,


(或由X服从超几何分布,
考查方向
解题思路
(1)根据走读生和住宿生的样本数完成表格,并由表格计算K2确定相关程度
(2)首先计算出第①组、第②组、第③组各抽取的人数,再确定随机变量X的所有可能取值并计算其概率完成分布列,最后计算数学期望。
易错点
各组人数的确定和离散型随机变量的概率的计算
已知函数f(x)=lnx-ax+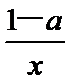
25.求函数f(x)的单调递增区间;
26.当a∈(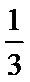
正确答案
(1)a≤0时,单调递增区间为(1,+∞);0<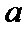
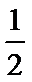
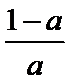
a=
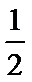
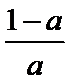
a>1时, 单调递增区间为(0,1).
解析
解:(1)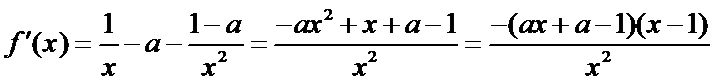
令
当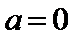
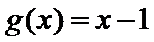
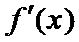
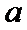
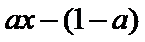
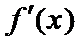
当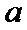
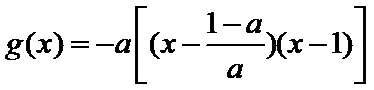
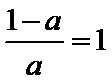
当0<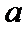
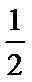
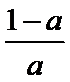
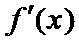
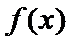
当a= 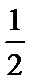
当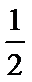
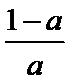
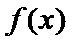
当a>1时,x∈(0,1)时,f'(x)>0,f(x)单调递增.
综上所述, a≤0时,单调递增区间为(1,+∞);
0<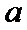
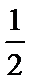
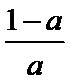
a=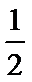
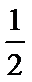
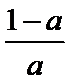
a>1时, 单调递增区间为(0,1).
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
正确答案
(2)
解析
解:
(2)由题知函数
①当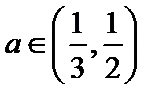
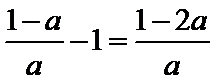
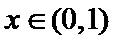
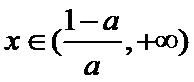
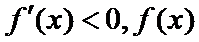
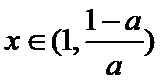
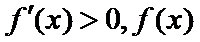
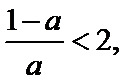
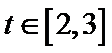
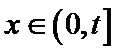
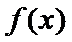
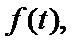
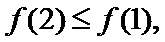
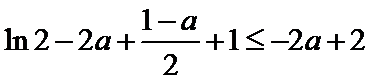
②当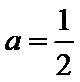
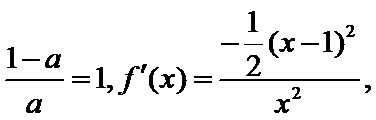
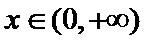
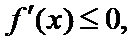
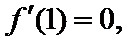
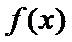
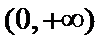
③当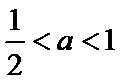
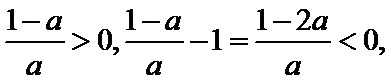
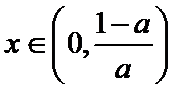
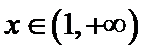
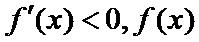
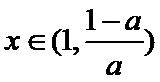
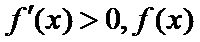
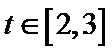
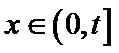
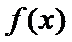
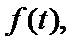
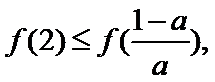
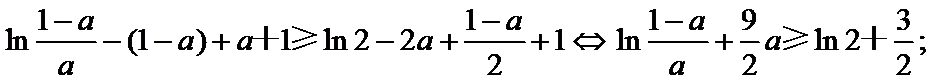
所以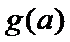
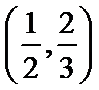
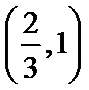
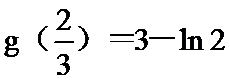
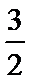
综上所述: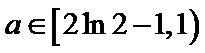
考查方向
解题思路
(1)对函数进行求导,再对会影响导数符号的部分进行分类讨论;从而探索其单调性(2)由(1)对a进行分段探讨函数的单调性及在(0,t]上的最小值情况,从而确定参数的取值范围。
易错点
对参数a分类不清晰,对多个参数处理思路乱。
请考生在以下3题中任选一题做答,如果多做,则按所做的第一题记分.做答时请用2B铅笔在答题卡上把所选题目对应的题号涂黑.
【选修4—1:几何证明选讲】请回答27、28题。
如图(8),圆O1与圆O2相交于A、B两点, AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点.
【选修4—4:坐标系与参数方程】请回答29、30题。
在直角坐标系xOy中,曲线C1的参数方程为

【选修4—5:不等式选讲】请回答31、32题。
设f(x)=|x-a|,(a∈R).
27.求证:PA·PD=PE·PC;
28.求证:AD=AE.
29.求曲线C1和曲线C2的极坐标方程;
30.已知射线l1:θ=α(0<α<


31.当-2≤x≤3时,f(x)≤4成立,求实数a的取值范围;
32.若存在实数x,使得f(x-a)-f(x+a)≤2a-1成立,求实数a的取值范围.
正确答案
(1)PA·PD=PE·PC;
解析
.解:(1) 

又

由①,②得
考查方向
解题思路
(1)由



(2)连接AC,DE,易知

易错点
易忽视
正确答案
(2)AD=AE
解析
解:
(2)连接AC,DE, 

由(1)知,
AB是⊙O2的直径,
考查方向
解题思路
(1)由



(2)连接AC,DE,易知

易错点
易忽视
正确答案
(1)


解析
.解:(1)曲线


曲线


考查方向
解题思路
(1)先把参数方程转化为直角坐标方程再转化为极坐标方程;(2)射线l1和l2恰好过极点,所以|OP|·|OQ|
易错点
对|OP|·|OQ|
正确答案
(2)
解析
解:
(2)设点

点

则


当


考查方向
解题思路
(1)先把参数方程转化为直角坐标方程再转化为极坐标方程;(2)射线l1和l2恰好过极点,所以|OP|·|OQ|
易错点
对|OP|·|OQ|
正确答案
(1)
解析
解:(1) 



即
考查方向
解题思路
(1)用公式法解含一个绝对值不等式;(2)存在实数x,使得f(x-a)-f(x+a)≤2a-1成立,则

易错点
难以转化合理转化条件
正确答案
(2)
解析
解:
(2)
又







综上所述,实数
考查方向
解题思路
(1)用公式法解含一个绝对值不等式;(2)存在实数x,使得f(x-a)-f(x+a)≤2a-1成立,则

易错点
难以转化合理转化条件