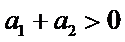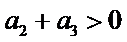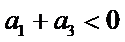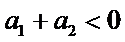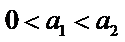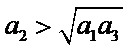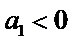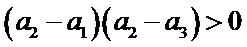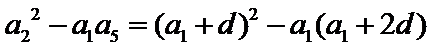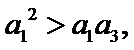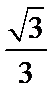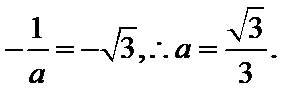- 真题试卷
- 模拟试卷
- 预测试卷
4.设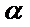
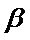
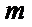
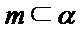
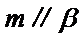
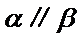
正确答案
解析
因为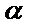
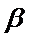
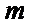
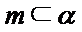
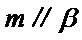
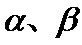
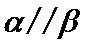
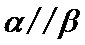
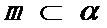
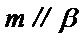
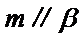
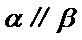
考查方向
解题思路
m∥β并得不到α∥β,根据面面平行的判定定理,只有α内的两相交直线都平行于β,而α∥β,并且m⊂α,显然能得到m∥β,这样即可找出正确选项.
易错点
命题关系的理解运用
知识点
7.如图,函数


正确答案
解析
如图所示,把函数



考查方向
解题思路
在已知坐标系内作出y=log2(x+1)的图象,利用数形结合得到不等式的解集.
易错点
函数图象平移的规律
知识点
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )
正确答案
解析
“燃油效率”是指汽车每消耗1升汽油行驶的里程,A中乙车消耗1升汽油,最多行驶的路程为乙车图象最高点的纵坐标值,A错误;B中以相同速度行驶相同路程,甲燃油效率最高,所以甲最省油,B错误,C中甲车以80千米/小时的速度行驶1小时,甲车每消耗1升汽油行驶的里程10km,行驶80km,消耗8升汽油,C错误,D中某城市机动车最高限速80千米/小时. 由于丙比乙的燃油效率高,相同条件下,在该市用丙车比用乙车更省油,故选D.
考查方向
解题思路
本题考查对新定义“燃油效率”的理解和读图能力,本题属于中等题,有能力要求,贴近学生生活,要求按照“燃油效率”的定义,汽车每消耗1升汽油行驶的里程,可以断定“燃油效率”高的车省油,相同的速度条件下,“燃油效率”高的汽车,每消耗1升汽油行驶的里程必然大,需要学生针对四个选择只做出正确判断.
易错点
正确的视图能力
知识点
1.复数
正确答案
解析
根据复数乘法运算计算得:
考查方向
解题思路
数的概念的扩充部分主要知识点有:复数的概念、分类,复数的几何意义、复数的运算,特别是复数的乘法与除法运算,运算时注意
易错点
复数运算性质
知识点
5.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
正确答案
解析
根据三视图恢复成三棱锥







考查方向
解题思路
本题考查三视图及多面体的表面积,本题属于基础题,正确利用三视图还原为原几何体,特别是有关数据的还原,另外要利用线面垂直的性质,判断三角形的形状,特别是侧面
易错点
本题考查了空间几何体的三视图的运用,空间想象能力,计算能力,关键是恢复直观图,得出几何体的性质.
知识点
6.设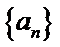
正确答案
解析
先分析四个答案支,A举一反例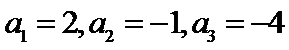
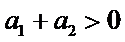
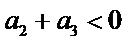
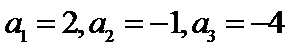
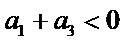
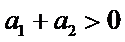
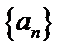
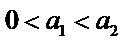
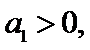
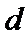
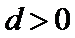
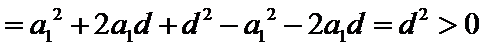
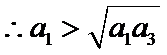
考查方向
解题思路
由于前两个选项无法使用公式直接做出判断,因此学生可以利用举反例的方法进行排除,这需要学生不能死套公式,要灵活应对,作差法是比较大小常规方法,对判断第三个选择只很有效.
易错点
等差数列性质的正确理解
知识点
3.执行如图所示的程序框图,输出的结果为( )
正确答案
解析
运行程序:










考查方向
解题思路
本题考查程序框图的程序运行,本题为基础题,掌握循环程序的运行方法,框图以赋值框和条件框为主,按照框图箭线方向和每个框的指令要求运行,注意条件框的要求是否满足,运行程序时要准确.
易错点
判断框的理解运用
知识点
2.若



正确答案
解析
如图,先画出可行域,由于





考查方向
解题思路
本题考查线性规划解题的基本方法,本题属于基础题,要求依据二元一次不等式组准确画出可行域,利用线性目标函数中直线的纵截距的几何意义,令


易错点
取得最值点的坐标
知识点
9.在

正确答案
40
解析
利用通项公式,



考查方向
解题思路
写出二项式定理展开式的通项公式,利用x的指数为3,求出r,然后求解所求数值.
易错点
二项式通项公式正确运用
知识点
11.在极坐标系中,点

正确答案
1
解析
先把点




考查方向
解题思路
本题考查极坐标基础知识,要求学生使用互化公式熟练进行点的坐标转化及曲线方程的转化,然后利用点到直线距离公式求出距离,本题属于基础题,先把点的极坐标化为直角坐标,再把直线的极坐标方程化为直角坐标方程,最后求点到直线的距离.
易错点
极坐标方程与普通方程的转化
知识点
10.已知双曲线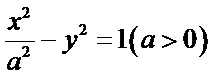

正确答案
解析
双曲线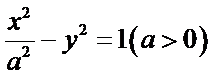
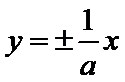
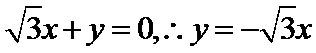
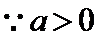
考查方向
解题思路
本题考查双曲线的几何性质,重点考查双曲线的渐近线方程,本题属于基础题,正确利用双曲线的标准方程,求出渐近线方程,求渐近线方程的简单方法就是把标准方程中的“1”改“0”,利用已知渐近线方程,求出参数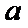
易错点
渐近线方程的准确运用
知识点
13.在







正确答案
解析
特殊化,不妨设







考查方向
解题思路
本题考查平面向量的有关知识及及向量运算,利用向量相等条件求值,本题属于基础题.利用坐标运算要建立适当的之间坐标系,准确写出相关点的坐标、向量的坐标,利用向量相等,列方程组,解出未知数的值.
易错点
准确写出相关点的坐标、向量的坐标
知识点
12.在




正确答案
1
解析

考查方向
解题思路
题目所求分式的分子为二倍角正弦,应用二倍角的正弦公式进行恒等变形,变形后为角的正弦、余弦式,灵活运用正弦定理和余弦定理进行角化边,再把边长代入求值.
易错点
灵活使用正弦定理、余弦定理进行边化角、角化边.
知识点
14.设函数
①若

②若

正确答案
(1)1,(2)

解析
①







(2)①若函数









②若函数




















考查方向
解题思路
本题考点为函数的有关性质,涉及函数图象、函数的最值,函数的零点、分类讨论思想解题.利用函数图象研究函数的单调性,求出函数的最值,涉计参数问题,针对参数进行分类讨论.
知识点
已知函数
15.求
16.求

正确答案
(Ⅰ)
解析
试题分析:先用降幂公式和辅助角公式进行三角恒等变形,把函数化为



考查方向
解题思路
本题考查三角函数式的恒等变形,本题属于基础题,要求准确应用降幂公式和辅助角公式进行变形,化为标准的
易错点
三角函数恒等变换公式的灵活运用.
正确答案
(Ⅱ)
解析
试题分析:由于





(Ⅱ)


考查方向
解题思路
本题考查三角函数的图象与性质,本题属于基础题,化为标准的
易错点
注意函数的定义域,求最值要给出自变量的取值,整体法求解三角函数最值.




假设所有病人的康复时间互相独立,从



人记为乙.
17.求甲的康复时间不少于14天的概率;
18.如果
19.当


正确答案
(Ⅰ)
解析
试题分析:针对甲有7种情况,康复时间不少于14天有3种情况,概率为
(Ⅰ)甲有7种取法,康复时间不少于14天的有3种取法,所以概率
考查方向
解题思路
本题考查古典概型和样本的方差,本题属于基础题,利用列举法准确列举事件的种数,求出概率.
易错点
准确列举基本事件.
正确答案
(Ⅱ)
考查方向
解题思路
本题考查古典概型,属于基础题,利用列举法准确列举事件的种数,求出概率.【解析】试题分析:如果
(Ⅱ) 如果





易错点
对立事件概率求解;准确列举基本事件;根据方差定义解方程
正确答案
(Ⅲ)
解析
试题分析:由于A组数据为10,11,12,13,14,15,16;B组数据调整为





(Ⅲ)把B组数据调整为



考查方向
解题思路
根据方差反应样本波动的大小,求出未知量.
易错点
根据方差定义解方程
如图,在四棱锥









20.求证:
21.求二面角
22.若


正确答案
(Ⅰ)略.
解析
试题分析:证明线线垂直可寻求线面垂直,利用题目提供的面面垂直平面


(Ⅰ)由于平面









考查方向
解题思路
本题考查线线、线面垂直及求二面角的相关知识及运算,本题属于中档题,熟练利用有关垂直的判定定理和性质定理进行面面垂直、线面垂直、线线垂直之间的转化与证明.
易错点
线线垂直的转化.
正确答案
(Ⅱ)
解析
试题分析:建立空间直角坐标系,写出相关点的坐标,平面AEF的法向量易得,只需求平面AEB的法向量,设平面AEB的法向量,利用线线垂直,数量积为零,列方程求出法向量,再根据二面角公式求出法向量的余弦值.
(Ⅱ)取CB的中点D,连接OD,以O为原点,分别以




















考查方向
解题思路
本题考查求二面角的相关知识及运算,本题属于中档题,利用空间向量解题时,要建立适当的直角坐标系,准确写出空间点的坐标,利用法向量求二面角.
易错点
平面法向量的求解.
正确答案
(Ⅲ)
解析
试题分析:由于





(Ⅲ)由(Ⅰ)知











考查方向
解题思路
本题考查利用数量积为零,解决线线、线面垂直问题.
易错点
平面向量坐标运算与函数性质的灵活运用.
已知函数
23.求曲线

24.求证:当

25.设实数



正确答案
(Ⅰ)
解析
试题分析:利用导数的几何意义,求出函数在
(Ⅰ)



考查方向
解题思路
本题考查导数的几何意义,第一步为基础,首先利用导数的几何意义求出切线斜率和切点坐标,写出切线方程.
易错点
导数的几何意义
正确答案
(Ⅱ)略.
解析
试题分析:要证明不等式






(Ⅱ)当











考查方向
解题思路
本题考查利用导数研究函数的单调性,证明不等式.
易错点
构造函数的单调性与原函数之间的关系.
正确答案
(Ⅲ)
解析
试题分析:构造函数研究函数单调性,但需要对参数



(Ⅲ)使




当


当

0
+
极小值

综上所述可知:
考查方向
解题思路
本题考查作差法构造函数,利用导数研究函数的单调性,证明不等式,对参数
易错点
函数单调性的灵活运用.
已知椭圆








26.求椭圆



27.设










正确答案
(Ⅰ)

解析
试题分析:(I)根据椭圆的几何性质得出得到椭圆中长半轴,短半轴,半焦距之间的关系求解即可.
(Ⅰ)由于椭圆












考查方向
解题思路
本题考查双曲线的几何性质,重点考查双曲线的渐近线方程,本题属于基础题,正确利用双曲线的标准方程,求出渐近线方程,求渐近线方程的简单方法就是把标准方程中的“1”改“0”,利用已知渐近线方程,求出参数
易错点
椭圆的几何性质
正确答案
(Ⅱ)存在点
解析
试题分析:(II)求解得出M,N点坐标,运用图形得出
(Ⅱ)







则







考查方向
解题思路
根据直线与椭圆的位置关系,设出点M,N坐标,然后根据几何关系结合坐标运算求得点Q的坐标即可证明问题.
易错点
角相等于斜率的关系
已知数列




28.若

29.若集合

30.求集合
正确答案
(Ⅰ)
解析
试题分析:(Ⅰ)

(Ⅰ)由已知
考查方向
解题思路
即考查了数列(分段形函数)求值,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题.
易错点
分段函数形数列通项公式求值.
正确答案
(Ⅱ)证明见解析;
解析
试题分析:(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设ak是3的倍数,由
(Ⅱ)因为集合














考查方向
解题思路
考查了归纳法证明和对数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题.
易错点
归纳法证明.
正确答案
(III )8.
解析
试题分析:(Ⅲ)分a1是3的倍数与a1不是3的倍数讨论,即可求得集合M的元素个数的最大值.
(Ⅲ)由于







①若



②







考查方向
解题思路
考查了数据的分析研究,考查了学生的分析问题能力和逻辑推理能力,本题属于拔高难题,适合选拔优秀学生.
易错点
数列元素分析.