- 真题试卷
- 模拟试卷
- 预测试卷
2．下列四个命题中，不正确的是（ ）
A若函数
B
C函数
D若函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1．复数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．将函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．若抛物线
A
B
C
D4
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．线段AB上的一点C，直线AB外一点P，满足
A1
B2
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．正四棱锥P—ABCD的五个顶点在同一个球面上，若其底面边长为4，侧棱长为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．函数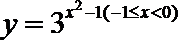
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．某电视台连续播放6个广告，其中有3个不同的商业广告，两个不同的奥运宣传广告，一个公益广告，要求最后播放的不能是商业广告，且奥运宣传广告与公益广告不能连续播放，两个奥运宣传广告也不能连续播放，则不同的播放方式的种数是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．在等比数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．设
A2
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．在二项式
正确答案
1
解析
解析已在路上飞奔，马上就到！
知识点
11．已知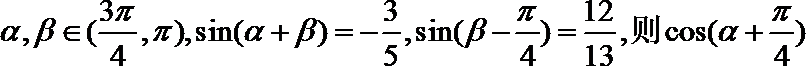
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．给出下列命题：
①函数
②在R上连续的函数
③已知函数
④底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥
⑤若P为双曲线
其中正确的命题是_________（把所有正确的命题的选项都填上）
正确答案
①③
解析
解析已在路上飞奔，马上就到！
知识点
13．将正奇数排列如下表，其中第i行第j个数表示成
正确答案
60
解析
解析已在路上飞奔，马上就到！
知识点
14．某实验室需购某种化工原料106千克，现在市场上该原料有两种包装，一种是每袋35千克，价格为140元，另一种是每袋24千克，价格为120元，在满足需要的条件下，最少要花费_______元。
正确答案
500
解析
解析已在路上飞奔，马上就到！
知识点
21．已知点P在曲线
（I）求
（II）设数列
（III）在（II）的条件下，当
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
17．在某校组织的一次篮球定点投篮比赛中，两人一对一比赛规则如一上：若某人某次投篮命中，则由他继续投篮，否则由对方接替投篮，现由甲、乙两人进行一对一投篮比赛，甲和乙每次投篮命中的概率分别是
（I）求3次投篮的人
（II）若投篮命中一次得1分，否则得0分，用
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．已知椭圆C的中点在原点，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|=2，点
（I）求椭圆C的方程；
（II）过F1的直线l与椭圆C相交于A，B两点，
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（I）当
（II）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．在斜三棱柱ABC—A1B1C1中，侧面A1ACC1⊥底面ABC，底面△ABC是边长为2的正三角形，A1A=A1C，A1A⊥A1C。
（1）求证：A1C1⊥B1C；
（2）求二面角B1—A1C—C1的大小。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．已知函数
（1）若函数
（2）设
正确答案
解析
解析已在路上飞奔，马上就到！