- 真题试卷
- 模拟试卷
- 预测试卷
9.在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知定义在区间


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知




① 使


② 函数


③ 
④ 设函数

其中正确的命题有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.2014年西安地区特长生考试有8所名校招生,若某3位同学恰好被其中的2 所名校录取,则不同的录取方法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下图是计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知O,A,M,B为平面上四点,且
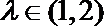
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
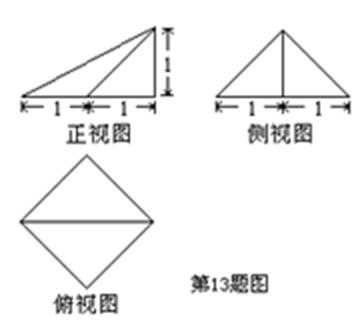
12.若

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.一个几何体的三视图如图所示,则该几何体的体积为____.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.复数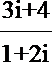
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
14.在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某市公租房的房源位于
(Ⅰ)恰有2人申请
(Ⅱ)申请的房源所在片区的个数
正确答案
(Ⅰ)所有可能的申请方式有


从而恰有2人申请

(Ⅱ)




综上知, 
从而有
解析
解析已在路上飞奔,马上就到!
知识点
18.在直三棱柱ABC -A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
(Ⅰ) 若D是AB中点,求证:AC1∥平面B1CD;
(Ⅱ)当

正确答案
(Ⅰ)
证明:连结BC1,交B1C于E,连接DE.
因为 直三棱柱ABC-A1B1C1,D是AB中点,
所以 侧面B B1C1C为矩形,DE为△ABC1的中位线,所以 DE// AC1.
因为 DE

(Ⅱ)
由(Ⅰ)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.
则B (3, 0, 0),A (0, 4, 0),A1 (0, 4, 4),B1 (3, 0, 4).设D (a, b, 0)(

因为 点D在线段AB上,且

所以




平面BCD的法向量为

由


所以 



所以二面角

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(I)求函数

(Ⅱ)对


正确答案

(I)



解析
解析已在路上飞奔,马上就到!
知识点
16. 已知函数
(Ⅰ)求函数


(Ⅱ)已知




正确答案
(Ⅰ)

∴函数




故

(Ⅱ)由题意,



在

由


∴当

解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列

(Ⅰ)证明:数列

(Ⅱ)设
正确答案
(Ⅰ)证明:由


即


又


(Ⅱ)
∴
=
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆





(I)求椭圆方程;
(Ⅱ)若





(III)在(Ⅱ)的条件下,试问




正确答案
(I)



(Ⅱ)


直线


代入椭圆





(III)设存在


解析
解析已在路上飞奔,马上就到!
知识点
15.选做题(请在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)。
(1)(坐标系与参数方程)已知直线的参数方程为




(2)(几何证明选讲)如右图,直线










(3)(不等式选讲)若存在实数


正确答案
(1) 
(2)
(3)
解析
解析已在路上飞奔,马上就到!