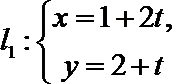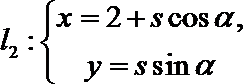理科数学佛山市2012年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共8小题，每小题5分，共40分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3.给出如下四个命题：

①若“且”为假命题，则、均为假命题；

②命题“若，则”的否命题为“若，则”；

③“”的否定是“”；

④若，则.

其中不正确的命题的个数是（）

正确答案

解析

②④正确

知识点

四种命题及真假判断

题型：单选题

分值: 5分

4. 三棱柱的侧棱与底面垂直，且底面是边长为2的等边三角形.若三棱柱的正视图（如图所示）的面积为8，则侧视图的面积为（）

正确答案

解析

设正视图的一边长为，则，所以.侧视图是一个矩形，一边长为4，另一边是三棱柱底面等边三角形的高，为，所以侧视图的面积为.故选C.

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

6. 设F是抛物线C1：y2＝2px（p＞0）的焦点，点A是抛物线与双曲线C2：（a＞0，b＞0）的一条渐近线的一个公共点，且AF⊥x轴，则双曲线的离心率为（）

正确答案

解析

依题意：A点的横坐标为,把代入双曲线渐近线方程得A点纵坐标为即|AF|= ,又因为|AF|=P,那么,即,那么双曲线离心率e=

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

7．某公司生产某种产品，固定成本为20 000元，每生产一单位产品，成本增加100元，已知总营业收入R与年产量x的关系是R=R(x)=则总利润最大时，每年生产的产品数是（）

A100

B150

C200

D300

正确答案

解析

由题意得，总成本函数为C＝C(x)＝20000＋100x，所以总利润函数为P＝P(x)＝R(x)－C(x)＝而P′(x)＝令P′(x)＝0，得x＝300，易知x＝300时，P最大．

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

5. 已知平面向量、为三个单位向量，且.满足(),则x+y的最大值为（）

正确答案

解析

【解法一】∵ ∴∴,要使x+y最大，必须使得x>0,y>0，那么即x+y≤ 当且仅当x=y=时达到最大值。【解法二】：可设,那么x+y=

知识点

二次函数的应用

题型：单选题

分值: 5分

2. 如图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图，若80分以上为优秀，根据图形信息可知：这次考试的优秀率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

频率分布直方图

题型：单选题

分值: 5分

8．设，若恒成立，则k的最大值为（）

正确答案

解析

由题可知k的最大值即为的最小值.又，取等号的条件是当且仅当，即，故的最大值为8.故选C.

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

1. 已知集合A＝{－1，0，1}，，则A∩B等于（）

A{1}

B{-1，1}

C{1，0}

D{-1，0，1}

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

填空题本大题共6小题，每小题5分，共30分。把答案填写在题中横线上。

题型：填空题

分值: 5分

9.计算：=__________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

10. 已知cos 31°＝m，则sin 239°·tan 149°的值是________

正确答案

解析

sin 239°·tan 149°＝sin (270°－31°)·tan (180°－31°)＝－cos 31°·(－tan 31°)＝cos 31°·tan 31°＝sin 31°＝

知识点

任意角的概念

题型：填空题

分值: 5分

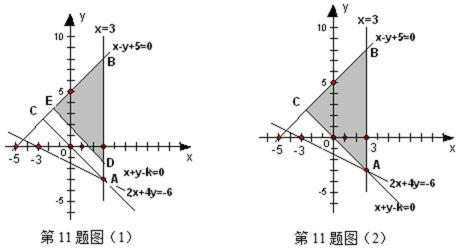
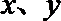
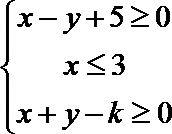
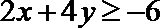
11. 若满足不等式组时，恒有，则k的取值范围是________ .

正确答案

k≥0

解析

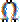
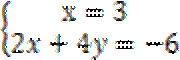
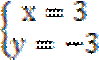
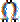
依题意，不等式组表示的区域如图（1），（2）中阴影部分所示，其中A点坐标是方程组解为则A((3,-3),B(3,8),DE直线方程为x+y-k=0,它与x=3的交点D的坐标为（3，k-3）因为不等式2x+4y≥-6解的区域是直线2x+4y=-6把坐标平面分成的两个半平面中的斜上半平面。那么，要使区域使得2x+4y≥-6恒成立，就是要区域内的所有点（x,y）都要在直线2x+4y=-6的斜上方，只要使k-3≥-3 即k≥0

知识点

一元二次不等式的解法

题型：填空题

分值: 5分

选做题（14 ~ 15题，只能从中选做一题）

14. （坐标系与参数方程选做题）

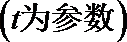
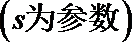
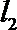
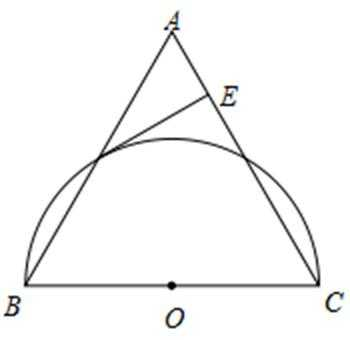
直线与直线平行，则直线的斜率为________.

15.（几何证明选讲选做题）

如图，在△ABC中，AB=AC，以BC为直径的半圆O与边AB相交于点D，切线DE⊥AC，垂足为点E．则_______________．

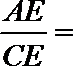
正确答案

14.

15.

解析

解析已在路上飞奔，马上就到！

知识点

坐标系的作用

题型：填空题

分值: 5分

13. 设M1(0，0)，M2(1，0)，以M1为圆心，| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2)，记作⊙M1；以M2为圆心，| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3)，记作⊙M2；……；

以Mn为圆心，| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1)，记作⊙Mn；……

当n∈N*时，过原点作倾斜角为30°的直线与⊙Mn交于An，Bn．考察下列论断：

当n＝1时，| A1B1 |＝2；

当n＝2时，| A2B2 |＝；

当n＝3时，| A3B3 |＝；

当n＝4时，| A4B4 |＝；

……

由以上论断推测一个一般的结论：对于n∈N*，| AnBn |＝___________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

分值: 5分

12. 在1，2，3，4，5，6，7的任一排列中，使相邻两数都互质的排列方式共有________种.(用数字作答)

正确答案

864

解析

先让数字1，3，5，7作全排列，有种，再排数字6，由于数字6不与3相邻，在排好的排列中，除3的左、右2个空隙，还有3个空隙可排数字6，故数字6[来有3种排法，最后排数字2，4，在剩下的4个空隙中排上2，4，有种排法，共有种.

知识点

由数列的前几项求通项

简答题（综合题）本大题共80分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16．若的图像与直线相切，并且切点横坐标依次成公差为的等差数列.

（1）求和的值；

（2）在⊿ABC中，a、b、c分别是∠A、∠B、∠C的对边。若是函数图象的一个对称中心，且a=4，求⊿ABC外接圆的面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

17. 某地农民种植A种蔬菜，每亩每年生产成本为7000元，A种蔬菜每亩产量及价格受天气、市场双重影响，预计明年雨水正常的概率为，雨水偏少的概率为 . 若雨水正常，A种蔬菜每亩产量为2000公斤，单价为6元/公斤的概率为，单价为3元/公斤的概率为; 若雨水偏少，A种蔬菜每亩产量为1500公斤，单价为6元/公斤的概率为，单价为3元/公斤的概率为.

（1）计算明年农民种植A种蔬菜不亏本的概率；

（2）在政府引导下，计划明年采取“公司加农户，订单农业”的生产模式，某公司未来不增加农民生产成本，给农民投资建立大棚，建立大棚后，产量不受天气影响，因此每亩产量为2500公斤，农民生产的A种蔬菜全部由公司收购，为保证农民的每亩预期收入增加1000元，收购价格至少为多少？

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 14分

18.如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC,AB=2,tan∠EAB=

（1）证明：平面ACD⊥平面ADE;

（2）当 AC=x时， V(x)表示三棱锥A-CBE的体积，当V(x)取得最大值时，求直线AD与平面ACE所成角的正弦值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 14分

21．设二次函数，对任意实数，有恒成立；数列满足.

（1）求函数的解析式和值域；

（2）试写出一个区间，使得当时，数列在这个区间上是递增数列，

并说明理由；

（3）已知，是否存在非零整数，使得对任意，都有恒成立，若存在，求之；若不存在，说明理由.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 14分

19.已知：函数在点（0，）处的切线与x-y-1=0平行, 且g(2)=,若为g(x)的导函数，设函数．

（1）求、的值及函数的解析式；

（2）如果关于的方程有三个相异的实数根，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 14分

20.已知椭圆和圆,过椭圆上一点引圆的两条切线，切点分别为．

（1）（ⅰ）若圆过椭圆的两个焦点，求椭圆的离心率的值；

（ⅱ）若椭圆上存在点，使得，求椭圆离心率的取值范围；

（2）设直线与轴、轴分别交于点，问当点P在椭圆上运动时，是否为定值？请证明你的结论．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的几何性质圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷