- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知集合
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
4. 下图程序运行结果是_____________
正确答案
21
解析
解析已在路上飞奔,马上就到!
知识点
5. 下图是七位评委打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为___________。
正确答案
85
解析
解析已在路上飞奔,马上就到!
知识点
6. 在120°的二面角内放置一个小球,它与二面角的两个面相切于A、B两点,这两个点的距离AB=5, 则小球的半径为______________
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
10. 对于使




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 若复数



正确答案
-6
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知条件






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 将直线



正确答案
-3或7
解析
解析已在路上飞奔,马上就到!
知识点
9. O是锐角



正确答案
内
解析
解析已在路上飞奔,马上就到!
知识点
11. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数f(x)是奇函数,且在[-1,1]是单调增函数,又f(-1)=-1, 则满足f(x)≤t2+2at+1对所有的x∈[-1,1]及a∈[-1,1]都成立的t的范围是__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知△ABC的周长为6, 
(1)求证:
(2)求△ABC的面积S的最大值;
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数f(x)=
(1)当a=4时,求集合A;
(2)当B=R时,求实数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直线B1C与平面ABC成30°角。
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求C1到平面B1AC的距离;
(3)求三棱锥A1-AB1C的体积。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如左图, B产品的利润与投资的算术平方根成正比,其关系如右图 (注:利润与投资单位:万元)。
(1)分别将A、B两种产品的利润表示为投资
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知点A(-1, 0)、B(1, 0),△ABC的周长为2+
(1)直接写出W的方程(不写过程);
(2)经过点(0, 


(3)设W的左右焦点分别为F1、 F2,点R在直线l:x-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 函数

(1)试求函数
(2)已知各项均为负数的数列



(3)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.已知正项数列


(1)证明:数列
(2)探究

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.四边形ABCD和四边形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设有3个投球手,其中一人命中率为q,剩下的两人水平相当且命中率均为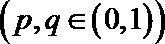
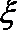
(1)当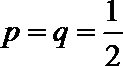
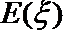
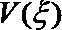
(2)当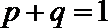
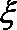
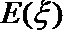
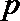
正确答案
解析
解析已在路上飞奔,马上就到!