- 真题试卷
- 模拟试卷
- 预测试卷
2.已知二次函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.对任意实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在极坐标中,由三条曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知定义域为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.建设服务政府要加强政府公共服务职能。以下体现履行这一职能的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
11.已知:



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
9.若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,在圆的内接四边形





正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.已知





正确答案
1.5
解析
解析已在路上飞奔,马上就到!
知识点
12.若不等式


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设
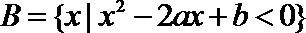
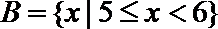
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知:函数

(Ⅰ)求证:函数


(Ⅱ)设



(ⅰ)当

(ⅱ)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知二次函数



(1)求函数
(2)若关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数








(1)求直线

(2)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.三个城市长沙、株洲、湘潭分别位于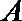
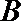
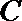
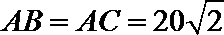
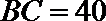
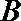
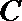
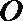
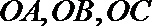
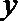
(Ⅰ)设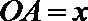
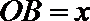
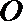
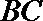

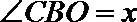

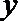

(Ⅱ)由(Ⅰ)中建立的函数关系,确定货运中转站的位置,使修建的道路的总长度最短.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.若对满足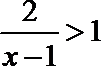

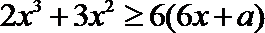

正确答案
解析
解析已在路上飞奔,马上就到!